Chào mừng bạn đến với bài học về Lý thuyết Đường trung bình của tam giác trong chương trình Toán 8. Đây là một phần kiến thức quan trọng, giúp bạn hiểu sâu hơn về các tính chất của tam giác và ứng dụng trong giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, cùng với các bài tập thực hành đa dạng để bạn có thể tự tin chinh phục môn Toán.
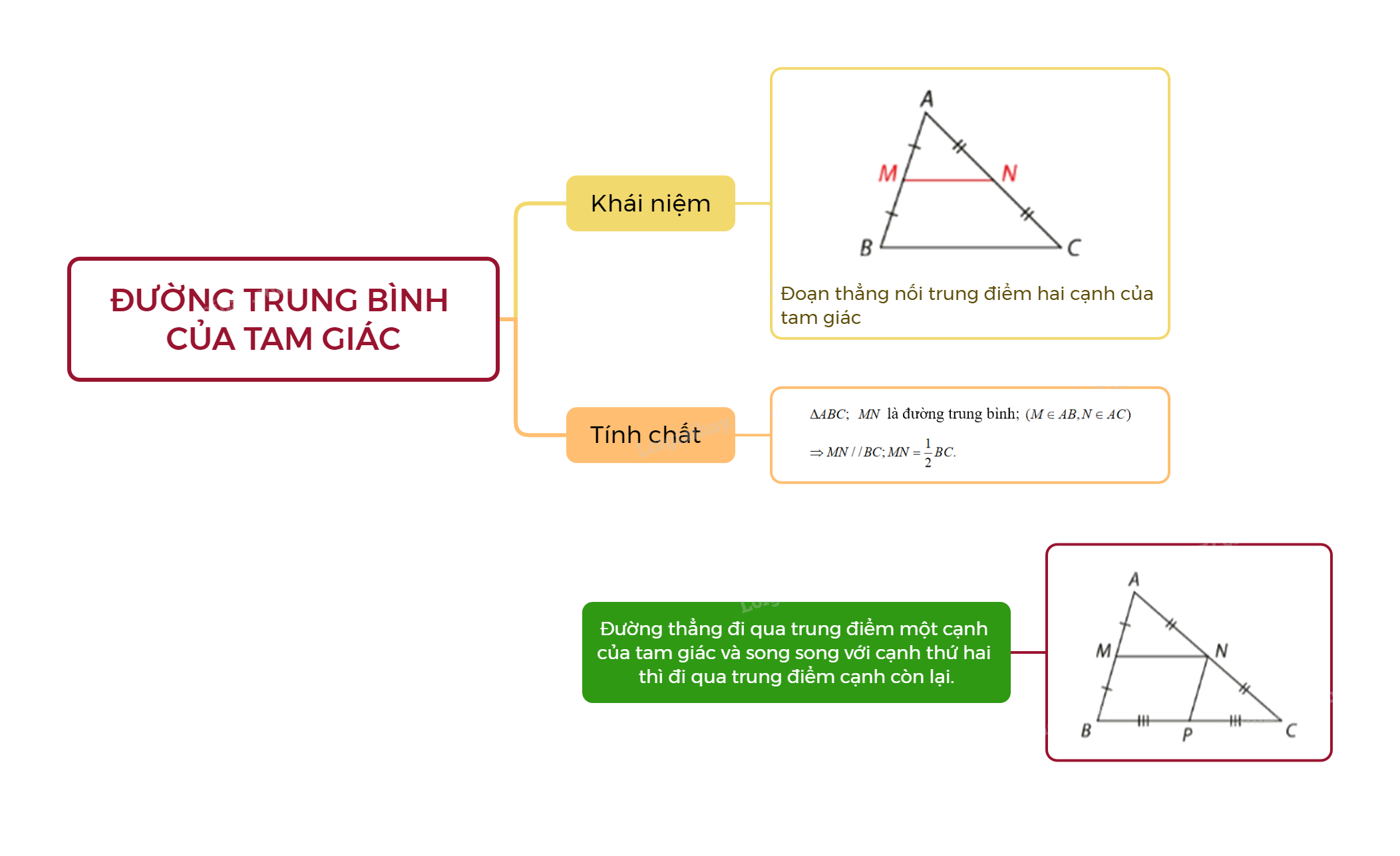
Đường trung bình là gì?
1. Khái niệm
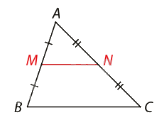
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
2. Tính chất đường trung bình của tam giác
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
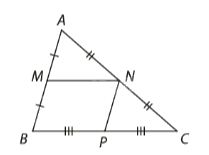
\(\Delta ABC;\) \(MN\) là đường trung bình; \((M \in AB,N \in AC)\)
\( \Rightarrow MN//BC;MN = \frac{1}{2}BC.\)
Nếu một đường thẳng đi qua trung điểm một cạnh của một tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh còn lại
Đường trung bình của tam giác là một khái niệm quan trọng trong hình học lớp 8, đóng vai trò then chốt trong việc chứng minh các tính chất liên quan đến tam giác. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết về lý thuyết này, bao gồm định nghĩa, tính chất, và các ứng dụng thực tế.
Trong một tam giác, đoạn thẳng nối trung điểm của hai cạnh là đường trung bình của tam giác đó. Ví dụ, xét tam giác ABC, nếu M là trung điểm của AB và N là trung điểm của AC, thì MN là đường trung bình của tam giác ABC.
Đường trung bình của tam giác có những tính chất quan trọng sau:
Chứng minh Tính chất 1 (MN // BC):
Xét tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Ta có:
Xét tam giác AMN và tam giác ABC, ta có:
Suy ra tam giác AMN đồng dạng với tam giác ABC (cạnh - góc - cạnh). Do đó, MN // BC.
Chứng minh Tính chất 2 (MN = 1/2 BC):
Vì tam giác AMN đồng dạng với tam giác ABC (chứng minh trên), ta có:
MN/BC = AM/AB = 1/2
Suy ra MN = 1/2 BC.
Đường trung bình của tam giác được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là:
Bài tập 1: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Biết BC = 10cm. Tính độ dài MN.
Giải:
Vì MN là đường trung bình của tam giác ABC nên MN = 1/2 BC = 1/2 * 10cm = 5cm.
Bài tập 2: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Biết MN song song với BC. Chứng minh rằng tam giác AMN đồng dạng với tam giác ABC.
Giải:
Vì MN // BC nên ∠AMN = ∠ABC (các góc so le trong) và ∠ANM = ∠ACB (các góc so le trong). Xét tam giác AMN và tam giác ABC, ta có:
Suy ra tam giác AMN đồng dạng với tam giác ABC (góc - góc - góc).
Ngoài hai tính chất cơ bản trên, đường trung bình của tam giác còn liên quan đến một số khái niệm khác như đường trung tuyến, trọng tâm của tam giác. Việc hiểu rõ mối liên hệ giữa các khái niệm này sẽ giúp bạn giải quyết các bài toán phức tạp hơn.
Lý thuyết Đường trung bình của tam giác là một phần kiến thức quan trọng trong chương trình Toán 8. Việc nắm vững định nghĩa, tính chất và ứng dụng của đường trung bình sẽ giúp bạn tự tin hơn trong việc giải các bài toán hình học. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.