Chào mừng các em học sinh đến với bài giải chi tiết bài 3.35 trang 88 SGK Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp phương pháp giải bài tập Toán 8 một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Bài 3.35 thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi sẽ hướng dẫn các em từng bước, từ việc phân tích đề bài đến việc đưa ra lời giải chính xác.
Chứng minh tam giác
Đề bài
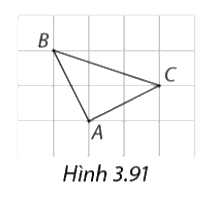
Chứng minh tam giác \(ABC\) vẽ trên giấy kẻ ô vuông (Hình 3.91) là tam giác vuông cân.
Phương pháp giải - Xem chi tiết
Dựa vào định lí Pythagore để chứng minh tam giác \(ABC\) là tam giác vuông cân.
Lời giải chi tiết
Gọi 1 ô li là 1 cm
Thì cạnh \(AB\) có số đo là:\(AB = \sqrt {{1^2} + {2^2}} = \sqrt 5 \) cm
Cạnh \(AC\) có số đo là: \(AC = \sqrt {{1^2} + {2^2}} = \sqrt 5 \)
Cạnh \(BC\) có số đo là: \(BC = \sqrt {{1^2} + {3^2}} = \sqrt {10} \)
Vậy \(ABC\) là tam giác cân tại \(A\).
Lại có \({\left( {\sqrt {10} } \right)^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {\sqrt 5 } \right)^2}\)
Vậy tam giác \(ABC\) là tam giác vuông cân tại \(A\).
Bài 3.35 trang 88 SGK Toán 8 yêu cầu học sinh vận dụng kiến thức về hình học, cụ thể là các tính chất của hình thang cân để giải quyết bài toán. Để giải bài này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Bài 3.35 thường liên quan đến việc chứng minh một tính chất nào đó của hình thang cân, hoặc tính toán độ dài các đoạn thẳng, góc trong hình thang cân. Ví dụ, bài toán có thể yêu cầu chứng minh rằng đường trung bình của hình thang cân bằng nửa tổng hai đáy, hoặc tính độ dài đường cao của hình thang cân khi biết độ dài hai đáy và cạnh bên.
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 3.35. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số gợi ý về cách giải:
Ví dụ minh họa (giả sử bài toán yêu cầu chứng minh đường trung bình của hình thang cân bằng nửa tổng hai đáy):
Gọi ABCD là hình thang cân với AB là đáy lớn và CD là đáy nhỏ. Gọi M và N lần lượt là trung điểm của AD và BC. Ta cần chứng minh MN = (AB + CD)/2.
Chứng minh:
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải toán, các em có thể làm thêm các bài tập sau:
Bài 3.35 trang 88 SGK Toán 8 là một bài tập quan trọng giúp các em hiểu sâu hơn về hình thang cân và các tính chất của nó. Bằng cách nắm vững các kiến thức và phương pháp giải bài tập, các em có thể tự tin giải quyết các bài toán tương tự trong các kỳ thi và bài kiểm tra.
| Kiến thức | Nội dung |
|---|---|
| Hình thang cân | Định nghĩa, tính chất, dấu hiệu nhận biết |
| Đường trung bình của hình thang | Định nghĩa, tính chất |
| Định lý Pitago | Nội dung, ứng dụng |
| Diện tích hình thang | Công thức tính diện tích |
Hy vọng với bài giải chi tiết này, các em sẽ hiểu rõ hơn về cách giải bài 3.35 trang 88 SGK Toán 8. Chúc các em học tập tốt!