Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 76, 77, 78 sách giáo khoa Toán 8.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Từ định nghĩa và tính chất của hình bình hành
Từ định nghĩa và tính chất của hình bình hành, ta có thể suy ra tính chất nào về cạnh, góc và đường chéo của hình thoi \(ABCD\)?
Phương pháp giải:
Áp dụng định nghĩa và tính chất của hình bình hành để suy ra tính chất về cạnh, góc và đường chéo của hình thoi \(ABCD\).
Lời giải chi tiết:
Trong hình thoi:
Có các cạnh bằng nhau
Có các cặp góc đối bằng nhau.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Hình thoi \(MNPQ\) có \(\widehat {NMQ} = 124^\circ \). Tính số đo góc \(MNQ\).
Phương pháp giải:
Áp dụng tính chất của hình thoi để tính số đo góc \(MNQ\).
Lời giải chi tiết:
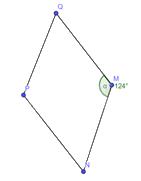
Gọi số đo góc \(MNQ\) là \(x\) =>\(\widehat {MNQ} = \widehat {MQN} = x\)
Xét tam giác cân \(QMN\), ta có:
\(\begin{array}{l}124^\circ + x + x = 180^\circ \\ = > x = \frac{{180^\circ - 124^\circ }}{2} = 28^\circ \end{array}\)
Vậy số đo góc \(MNQ\) là \(28^\circ \).
Cho hình thoi \(ABCD\) (Hình 3.66).
a) Tam giác \(ABC\) là tam giác gì?
b) Vì sao \(BO\) là đường trung tuyến của tam giác \(ABC\)?
c) Em rút ra thêm được tính chất gì về hai đường chéo của hình thoi?
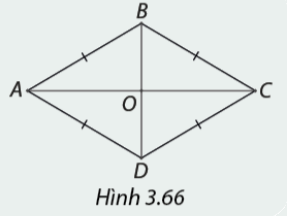
Phương pháp giải:
Dựa vào định nghĩa và các tính chất của hình bình hành và hình thoi để xác định.
Lời giải chi tiết:
a) Xét \(\Delta ABC\) ta có:
\(AB = BC\) (vì \(ABCD\) là hình thoi)
→ \(\Delta ABC\) là tam giác cân
b) Ta có:
\(AC\) và \(BD\) là hai đường chéo của hình thoi \(ABCD\)
Nên O là trung điểm của \(AC\) và \(BD\).
→ \(BO\) là đường trung tuyến của tam giác \(ABC\)
c) Vì \(BO\) là đường trung tuyến của tam giác \(ABC\)
Mà \(\Delta ABC\) là tam giác cân
→ \(BO \bot AC\)
→ Hai đường chéo của hình thoi vuông góc với nhau.
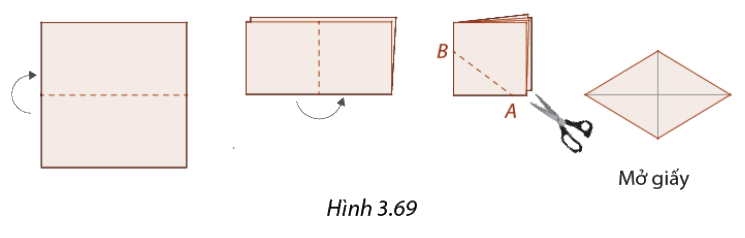
Gấp một tờ giấy làm tư như Hình 3.69 và cắt chéo theo đường \(AB\) bất kì (\(A,B\) nằm trên hai mép gấp). Sau khi mở giấy, tứ giác cắt được là hình gì? Vì sao?
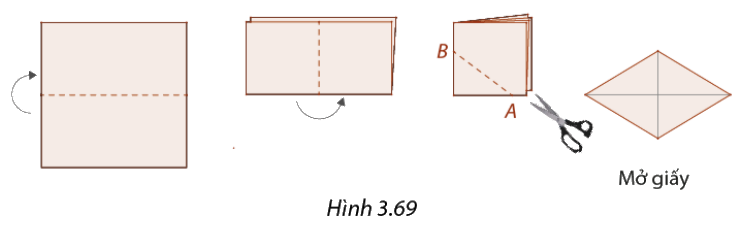
Phương pháp giải:
Dựa vào định nghĩa và tính chất của hình thoi để xác định.
Lời giải chi tiết:
Sau khi mở giấy, tứ giác cắt được là hình thoi.
Bởi vì khi gấp giấy làm bốn và cắt chéo một đường \(AB\) thì sẽ được 4 đường thẳng bằng \(AB\) và 4 đường thẳng đó chính là 4 cạnh của tứ giác sau khi mở giấy. Mà tứ giác có bốn cạnh bằng nhau là hình thoi.
Từ định nghĩa và tính chất của hình bình hành, ta có thể suy ra tính chất nào về cạnh, góc và đường chéo của hình thoi \(ABCD\)?
Phương pháp giải:
Áp dụng định nghĩa và tính chất của hình bình hành để suy ra tính chất về cạnh, góc và đường chéo của hình thoi \(ABCD\).
Lời giải chi tiết:
Trong hình thoi:
Có các cạnh bằng nhau
Có các cặp góc đối bằng nhau.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Cho hình thoi \(ABCD\) (Hình 3.66).
a) Tam giác \(ABC\) là tam giác gì?
b) Vì sao \(BO\) là đường trung tuyến của tam giác \(ABC\)?
c) Em rút ra thêm được tính chất gì về hai đường chéo của hình thoi?
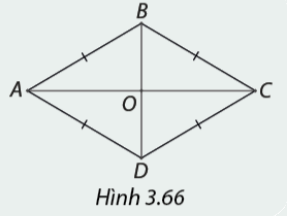
Phương pháp giải:
Dựa vào định nghĩa và các tính chất của hình bình hành và hình thoi để xác định.
Lời giải chi tiết:
a) Xét \(\Delta ABC\) ta có:
\(AB = BC\) (vì \(ABCD\) là hình thoi)
→ \(\Delta ABC\) là tam giác cân
b) Ta có:
\(AC\) và \(BD\) là hai đường chéo của hình thoi \(ABCD\)
Nên O là trung điểm của \(AC\) và \(BD\).
→ \(BO\) là đường trung tuyến của tam giác \(ABC\)
c) Vì \(BO\) là đường trung tuyến của tam giác \(ABC\)
Mà \(\Delta ABC\) là tam giác cân
→ \(BO \bot AC\)
→ Hai đường chéo của hình thoi vuông góc với nhau.
Hình thoi \(MNPQ\) có \(\widehat {NMQ} = 124^\circ \). Tính số đo góc \(MNQ\).
Phương pháp giải:
Áp dụng tính chất của hình thoi để tính số đo góc \(MNQ\).
Lời giải chi tiết:
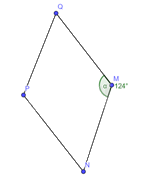
Gọi số đo góc \(MNQ\) là \(x\) =>\(\widehat {MNQ} = \widehat {MQN} = x\)
Xét tam giác cân \(QMN\), ta có:
\(\begin{array}{l}124^\circ + x + x = 180^\circ \\ = > x = \frac{{180^\circ - 124^\circ }}{2} = 28^\circ \end{array}\)
Vậy số đo góc \(MNQ\) là \(28^\circ \).
Gấp một tờ giấy làm tư như Hình 3.69 và cắt chéo theo đường \(AB\) bất kì (\(A,B\) nằm trên hai mép gấp). Sau khi mở giấy, tứ giác cắt được là hình gì? Vì sao?
Phương pháp giải:
Dựa vào định nghĩa và tính chất của hình thoi để xác định.
Lời giải chi tiết:
Sau khi mở giấy, tứ giác cắt được là hình thoi.
Bởi vì khi gấp giấy làm bốn và cắt chéo một đường \(AB\) thì sẽ được 4 đường thẳng bằng \(AB\) và 4 đường thẳng đó chính là 4 cạnh của tứ giác sau khi mở giấy. Mà tứ giác có bốn cạnh bằng nhau là hình thoi.
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của chúng là vô cùng quan trọng để giải quyết các bài tập liên quan.
Mục 2 thường bao gồm các nội dung sau:
Để giải các bài tập trong mục 2, các em cần:
Bài tập: Cho hình chữ nhật ABCD, AB = 8cm, BC = 6cm. Tính độ dài đường chéo AC.
Giải:
Vì ABCD là hình chữ nhật nên góc ABC vuông. Áp dụng định lý Pitago vào tam giác ABC, ta có:
AC2 = AB2 + BC2 = 82 + 62 = 64 + 36 = 100
Suy ra AC = √100 = 10cm.
Các bài tập trong mục 2 thường có các dạng sau:
Các em cần lưu ý những điều sau khi giải bài tập:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 76, 77, 78 SGK Toán 8. Chúc các em học tập tốt!