Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 44, 45 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và giải quyết các bài tập một cách hiệu quả.
Bài viết này sẽ cung cấp đáp án chính xác, dễ hiểu và phương pháp giải từng bài tập trong mục 2, giúp các em tự tin hơn khi làm bài tập về nhà và chuẩn bị cho các kỳ kiểm tra.
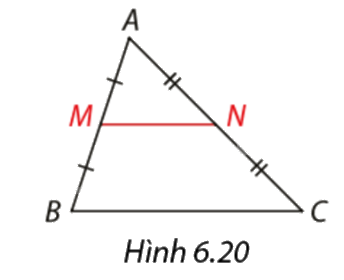
Xem hình 6.20. Giải thích vì sao đường trung bình \(MN\) song song với cạnh
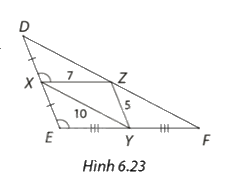
Trong Hình 6.23, giải thích vì sao \(Z\) là trung điểm của \(DF\) và tính độ dài ba cạnh tam giác \(DEF.\)
Phương pháp giải:
Dựa vào định lí Thales để giải thích vì sao Z là trung điểm của DF.
Dựa vào tính chất đường trung bình của tam giác: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Lời giải chi tiết:
Xét tam giác \(DEF\) , ta có:
\(\widehat {DXZ} = \widehat {DEY}\) (mà hai góc này ở vị trí đồng vị)
=> \(XZ//EF\)
Áp dụng định lí Thales ta có:
\(\frac{{DX}}{{XE}} = \frac{{DZ}}{{ZF}} = 1\)
=> Z là trung điểm của DF
Lại có:
\(\begin{array}{l}EX = XD\\EY = YF\end{array}\)
=> X là trung điểm của DE
Y là trung điểm của EF
=> XY là đường trung bình của tam giác \(DEF\) .
Áp dụng tính chất của đường trung bình của tam giác ta có:
\(\begin{array}{l}XY = \frac{1}{2}DF\\ = > DF = 10.2 = 20\end{array}\)
Mà Z là trung điểm của DF
Y là trung điểm của EF
=> ZY là đường trung bình của tam giác DEF
Áp dụng tính chất đường trung bình ta có:
\(\begin{array}{l}ZY = \frac{1}{2}DE\\ = > DE = 2.5 = 10\end{array}\)
Mà X là trung điểm của DE
Z là trung điểm của DF
=> XZ là đường trung bình
Áp dụng tính chất đường trung bình ta có:
\(\begin{array}{l}XZ = \frac{1}{2}EF\\EF = 2.7 = 14\end{array}\)
Vậy tam giác \(DEF\) có \(DF = 20,EF = 14,DE = 10\)
Xem hình 6.20. Giải thích vì sao đường trung bình \(MN\) song song với cạnh \(BC.\) Đo và tính tỉ số của \(MN\) và \(BC.\)
Phương pháp giải:
Sử dụng định lí Thalès đảo trong tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC.\)
Lời giải chi tiết:
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow MN//BC\) (định li Thalès đảo).
Xét tam giác \(ABC\) có \(MN//BC\) nên theo hệ quả định lí Thalès ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}.\)
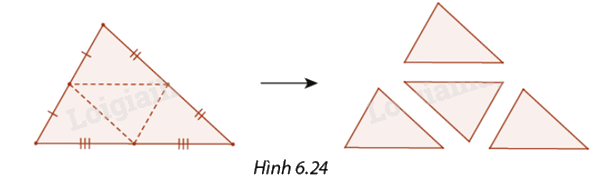
Giải thích vì sao khi cắt ba mảnh bìa hình tam giác theo ba đường trung bình của nó (Hình 6.24) thì ta được bốn tam giác bằng nhau.
Phương pháp giải:
Dựa vào tính chất đường trung bình của tam giác và các trường hợp hai tam giác bằng nhau để chứng minh.
Lời giải chi tiết:
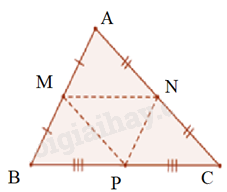
Xét tam giác \(AMN\) và \(BMP\) , ta có:
\(AM = BM\) (M là trung điểm)
\(MN = BP\) (do \(MN = BP = \frac{1}{2}BC\) )
\(MP = AN\) (do \(MP = AN = \frac{1}{2}AC\) )
=> \(\Delta AMN = \Delta BMP\left( {c - c - c} \right)\)
Chứng minh tương tự với các trường hợp còn lại. Ta được 4 tam giác bằng nhau.
Xem hình 6.20. Giải thích vì sao đường trung bình \(MN\) song song với cạnh \(BC.\) Đo và tính tỉ số của \(MN\) và \(BC.\)
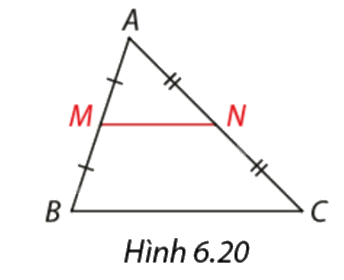
Phương pháp giải:
Sử dụng định lí Thalès đảo trong tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC.\)
Lời giải chi tiết:
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow MN//BC\) (định li Thalès đảo).
Xét tam giác \(ABC\) có \(MN//BC\) nên theo hệ quả định lí Thalès ta có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}.\)
Trong Hình 6.23, giải thích vì sao \(Z\) là trung điểm của \(DF\) và tính độ dài ba cạnh tam giác \(DEF.\)
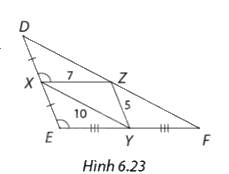
Phương pháp giải:
Dựa vào định lí Thales để giải thích vì sao Z là trung điểm của DF.
Dựa vào tính chất đường trung bình của tam giác: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Lời giải chi tiết:
Xét tam giác \(DEF\) , ta có:
\(\widehat {DXZ} = \widehat {DEY}\) (mà hai góc này ở vị trí đồng vị)
=> \(XZ//EF\)
Áp dụng định lí Thales ta có:
\(\frac{{DX}}{{XE}} = \frac{{DZ}}{{ZF}} = 1\)
=> Z là trung điểm của DF
Lại có:
\(\begin{array}{l}EX = XD\\EY = YF\end{array}\)
=> X là trung điểm của DE
Y là trung điểm của EF
=> XY là đường trung bình của tam giác \(DEF\) .
Áp dụng tính chất của đường trung bình của tam giác ta có:
\(\begin{array}{l}XY = \frac{1}{2}DF\\ = > DF = 10.2 = 20\end{array}\)
Mà Z là trung điểm của DF
Y là trung điểm của EF
=> ZY là đường trung bình của tam giác DEF
Áp dụng tính chất đường trung bình ta có:
\(\begin{array}{l}ZY = \frac{1}{2}DE\\ = > DE = 2.5 = 10\end{array}\)
Mà X là trung điểm của DE
Z là trung điểm của DF
=> XZ là đường trung bình
Áp dụng tính chất đường trung bình ta có:
\(\begin{array}{l}XZ = \frac{1}{2}EF\\EF = 2.7 = 14\end{array}\)
Vậy tam giác \(DEF\) có \(DF = 20,EF = 14,DE = 10\)
Giải thích vì sao khi cắt ba mảnh bìa hình tam giác theo ba đường trung bình của nó (Hình 6.24) thì ta được bốn tam giác bằng nhau.
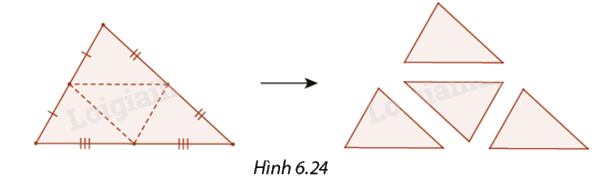
Phương pháp giải:
Dựa vào tính chất đường trung bình của tam giác và các trường hợp hai tam giác bằng nhau để chứng minh.
Lời giải chi tiết:
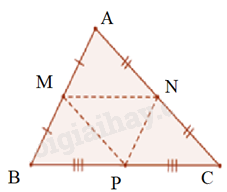
Xét tam giác \(AMN\) và \(BMP\) , ta có:
\(AM = BM\) (M là trung điểm)
\(MN = BP\) (do \(MN = BP = \frac{1}{2}BC\) )
\(MP = AN\) (do \(MP = AN = \frac{1}{2}AC\) )
=> \(\Delta AMN = \Delta BMP\left( {c - c - c} \right)\)
Chứng minh tương tự với các trường hợp còn lại. Ta được 4 tam giác bằng nhau.
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của chúng là vô cùng quan trọng để giải quyết các bài tập liên quan.
Mục 2 thường bao gồm các nội dung sau:
Để giải các bài tập trong mục này một cách hiệu quả, các em cần:
Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Đường thẳng DE cắt AC tại F. Chứng minh rằng AF = 2FC.
Giải:
Các bài tập trong mục 2 thường thuộc các dạng sau:
Khi giải các bài tập về tứ giác, các em cần chú ý:
Hy vọng với bài viết này, các em đã nắm vững kiến thức và kỹ năng giải các bài tập trong mục 2 trang 44, 45 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!