Chào mừng các em học sinh đến với bài học về Lý thuyết Tính chất đường phân giác trong của tam giác, chương trình Toán 8. Bài học này sẽ giúp các em hiểu rõ về định nghĩa, tính chất quan trọng của đường phân giác trong tam giác, cũng như cách áp dụng vào giải các bài tập thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp kiến thức Toán 8 một cách dễ hiểu, trực quan, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
Đường phân giác trong tam giác có tính chất gì?
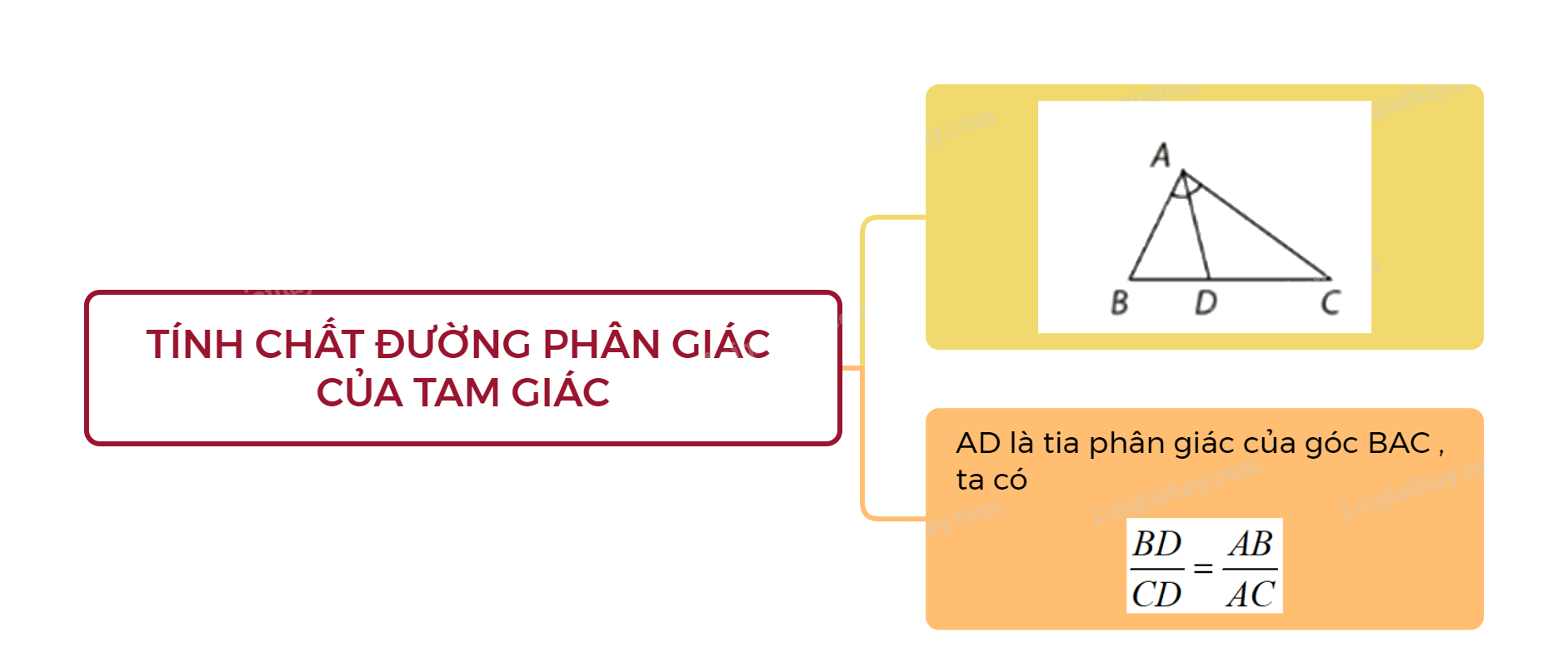
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
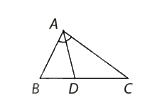
\(\Delta ABC;\) \(AD\) là đường phân giác của góc \(A\)\((D \in BC)\).
\( \Rightarrow \frac{{BD}}{{CD}} = \frac{{AB}}{{AC}}\).
Ví dụ:
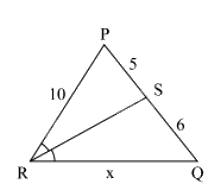
RS là tia phân giác của góc \(\widehat {PRQ}\). Sử dụng tính chất đường phân giác, ta có:
\(\begin{array}{l}\frac{{SQ}}{{SR}} = \frac{{RQ}}{{RP}}\\ \Leftrightarrow \frac{{10}}{5} = \frac{x}{6}\\ \Leftrightarrow 2 = \frac{x}{6}\\ \Leftrightarrow x = 12\end{array}\)
Vậy độ dài đoạn thẳng RQ là 12.
Đường phân giác trong của một tam giác là đoạn thẳng nối đỉnh của tam giác với một điểm trên cạnh đối diện, sao cho nó chia góc tại đỉnh đó thành hai góc bằng nhau. Đây là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học lớp 8.
Trong tam giác ABC, đường thẳng AD (với D nằm trên BC) được gọi là đường phân giác trong của góc A nếu ∠BAD = ∠CAD.
Tính chất quan trọng nhất của đường phân giác trong tam giác được thể hiện qua định lý sau:
Cụ thể, nếu AD là đường phân giác trong của tam giác ABC (D nằm trên BC) thì:
AB/AC = BD/DC
Để chứng minh định lý này, ta có thể sử dụng phương pháp chứng minh bằng tam giác đồng dạng. Kẻ đường thẳng CE song song với AD (E nằm trên AB kéo dài). Khi đó, ta có:
Vì ∠DAE = ∠CAD (do AD là phân giác) nên ∠AEC = ∠ACE, suy ra tam giác AEC cân tại E. Do đó, AE = AC.
Xét tam giác BDE và tam giác BAC, ta có:
Suy ra tam giác BDE đồng dạng với tam giác BAC (g.g). Từ đó, ta có tỉ lệ:
BD/BA = DE/AC
Mà DE = AE = AC, nên BD/BA = AC/AC = 1. Do đó, BD = BA. Tuy nhiên, cách chứng minh này có một sai sót nhỏ. Cách chứng minh đúng hơn sử dụng việc kẻ đường thẳng song song với AD từ C cắt AB tại E.
Tính chất này được sử dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác, đặc biệt là các bài toán về tỉ lệ đoạn thẳng. Ví dụ:
Bài tập 1: Cho tam giác ABC có AB = 6cm, AC = 9cm, BC = 12cm. AD là đường phân giác trong của góc A. Tính BD và DC.
Giải:
Áp dụng tính chất đường phân giác trong tam giác, ta có:
AB/AC = BD/DC
6/9 = BD/DC
BD/DC = 2/3
Mà BD + DC = BC = 12cm. Đặt BD = 2x, DC = 3x. Khi đó, 2x + 3x = 12cm, suy ra 5x = 12cm, x = 2.4cm.
Vậy BD = 2 * 2.4cm = 4.8cm và DC = 3 * 2.4cm = 7.2cm.
Ngoài đường phân giác trong, còn có đường phân giác ngoài của một góc trong tam giác. Đường phân giác ngoài của góc A là đường thẳng chia góc ngoài tại đỉnh A thành hai góc bằng nhau.
Để nắm vững kiến thức về tính chất đường phân giác trong tam giác, các em nên luyện tập thêm nhiều bài tập khác nhau. giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú, đa dạng, giúp các em rèn luyện kỹ năng giải toán một cách hiệu quả.
Hy vọng bài học này sẽ giúp các em hiểu rõ hơn về Lý thuyết Tính chất đường phân giác trong của tam giác. Chúc các em học tập tốt!