Chào mừng các em học sinh đến với bài giải chi tiết bài 6.29 trang 61 SGK Toán 8. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác và đầy đủ.
Cho tam giác \(ABC\) có \(\widehat B < \widehat C\).
Đề bài
Cho tam giác \(ABC\) có \(\widehat B < \widehat C\). Trên cạnh \(AB\), lấy điểm \(D\) sao cho \(\widehat {ACD} = \widehat B\). Cho \(AD = 5cm,BD = 15cm\) và \(CD = 12cm\).
a) Chứng minh rằng \(A{C^2} = AB.AD\)
b) Tính độ dài các cạnh của tam giác \(ABC\).
c) Tia phân giác của góc \(A\) cắt \(CD\) tại \(M\) và cắt \(BC\) tại \(N\). Tính tỉ số \(\frac{{AM}}{{AN}}\)
Phương pháp giải - Xem chi tiết
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
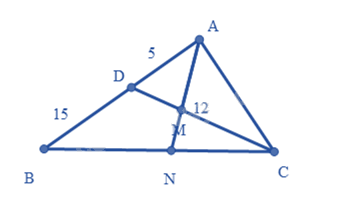
a) Xét hai tam giác \(ABC\) và tam giác \(ACD\), ta có:
\(\widehat A\) là góc chung
\(\widehat {ACD} = \widehat B\) (gt)
=> \(\Delta ABC\) ∽ \(\Delta ACD\) (g-g)
Ta có tỉ số đồng dạng:
\(\begin{array}{l}\frac{{AB}}{{AC}} = \frac{{AC}}{{AD}}\\ AB.AD = AC.AC\\ \\ A{C^2} = AB.AD\end{array}\)
b) Vì \(\Delta ABC\) ∽ \(\Delta ACD\) nên ta có:
\(\begin{array}{l}\;\frac{{AB}}{{AC}} = \frac{{AC}}{{AD}} = \frac{{BC}}{{CD}}\\ \Leftrightarrow \frac{{20}}{{AC}} = \frac{{AC}}{5} = \frac{{BC}}{{12}}\end{array}\)
Mà
\(\begin{array}{l}A{C^2} = AB.AD\\ \Rightarrow A{C^2} = 20.5\\ \Rightarrow A{C^2} = 100\\ \Rightarrow AC = 10\end{array}\)
Suy ra \(\frac{{AC}}{5} = \frac{{BC}}{{12}} \Leftrightarrow \frac{{10}}{5} = \frac{{BC}}{{12}} \Rightarrow BC = 24\)
Vậy tam giác \(ABC\) có độ dài các cạnh \(AB = 20;AC = 10;BC = 24\)
c) Xét tam giác \(AMD\) và tam giác \(ANC\), ta có:
\(\widehat {DAM} = \widehat {NAC}\) (do \(AN\) là tia phân giác góc A)
\(\widehat {ADM} = \widehat {ACN}\) (do \(\Delta ABC\) ∽ \(\Delta ACD\))
=> \(\Delta AMD\) ∽ \(\Delta ACN\) (g-g)
Ta có tỉ số đồng dạng:
\(\frac{{AM}}{{AN}} = \frac{{AD}}{{AC}} = \frac{5}{{10}} = \frac{1}{2}\)
Bài 6.29 trang 61 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hình chữ nhật, bao gồm:
Bài 6.29 thường yêu cầu học sinh chứng minh một tứ giác là hình chữ nhật dựa trên các điều kiện cho trước. Để làm được điều này, học sinh cần phân tích kỹ đề bài, xác định các yếu tố đã cho và lựa chọn dấu hiệu nhận biết hình chữ nhật phù hợp.
Dưới đây là hướng dẫn giải chi tiết bài 6.29 trang 61 SGK Toán 8. Lưu ý rằng, tùy thuộc vào từng đề bài cụ thể, phương pháp giải có thể khác nhau. Tuy nhiên, các bước cơ bản sau đây sẽ giúp học sinh tiếp cận bài toán một cách hiệu quả:
Đề bài: Cho tứ giác ABCD có góc A = 90o, góc C = 90o. Chứng minh rằng ABCD là hình chữ nhật.
Giải:
Để củng cố kiến thức về bài 6.29 trang 61 SGK Toán 8, học sinh có thể làm thêm các bài tập sau:
Để giải các bài tập về hình chữ nhật một cách hiệu quả, học sinh cần:
Bài 6.29 trang 61 SGK Toán 8 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hình chữ nhật và các ứng dụng của nó trong thực tế. Hy vọng rằng, với hướng dẫn chi tiết và các bài tập luyện tập trên đây, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán.