Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học và làm bài tập đôi khi gặp nhiều khó khăn. Do đó, chúng tôi đã biên soạn bộ giải chi tiết các bài tập trong SGK Toán 8, đặc biệt là mục 2 trang 38, 39, 40, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Giấy vở học sinh có các đường kẻ song song và cách đều nhau.
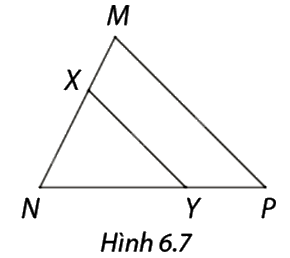
Trong hình 6.7, \(XY\) song song với \(MP.\) Em hãy cho biết tên đoạn thẳng ở các ô?.
\(\frac{{MX}}{{NX}} = \frac{?}{?};\frac{{NY}}{?} = \frac{?}{{MN}}.\)
Phương pháp giải:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
\(\begin{array}{l}\frac{{MX}}{{NX}} = \frac{{PY}}{{NY}};\\\frac{{NY}}{{NP}} = \frac{{NX}}{{MN}}\end{array}\)
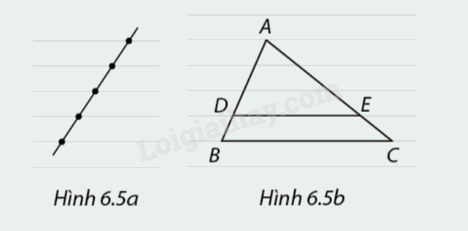
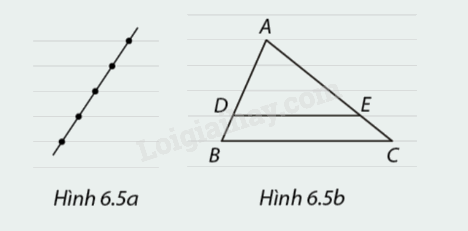
Giấy vở học sinh có các đường kẻ song song và cách đều nhau. Khi vẽ một đường thẳng bất kì cắt các đường kẻ, ta được các đoạn thẳng liên tiếp bằng nhau (Hình 6.5a). Xét \(\Delta ABC\) trong hình 6.5b.
1. Chọn \(BD\) làm đơn vị đo độ dài, em hãy tính độ dài \(AD,AB\) và các tỉ số \(\frac{{DA}}{{DB}},\frac{{AD}}{{AB}},\frac{{BD}}{{BA}}.\)
2. Chọn \(CE\) làm đơn vị đo độ dài, em hãy tính độ dài \(AE,AC\) và các tỉ số \(\frac{{EA}}{{EC}},\frac{{AE}}{{AC}},\frac{{CE}}{{CA}}.\)
3. So sánh các cặp tỉ số\(\frac{{DA}}{{DB}}\) và \(\frac{{EA}}{{EC}},\frac{{AD}}{{AB}}\) và \(\frac{{AE}}{{AC}},\frac{{BD}}{{BA}}\) và \(\frac{{CE}}{{CA}}.\) Em có nhận xét gì về các cặp đoạn thẳng được cho?
Phương pháp giải:
Tỉ số của hai đoạn thẳng AB và CD là tỉ số độ dài của chúng theo cùng một đơn vị đo, kí hiệu \(\frac{{AB}}{{CD}}\).
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
Lời giải chi tiết:
1. Chọn \(BD\) là đơn vị đo độ dài, ta có:
\(AD = 3\left( {BD} \right)\)
\(AB = 4\left( {BD} \right)\)
\(\begin{array}{l}\frac{{DA}}{{DB}} = \frac{3}{1} = 3\\\frac{{AD}}{{AB}} = \frac{3}{4} = 0,75\\\frac{{BD}}{{BA}} = \frac{1}{4} = 0,25\end{array}\)
2. Chọn \(CE\) làm đơn vị đo độ dài, ta có:
\(\begin{array}{l}AE = 3\left( {CE} \right)\\AC = 4\left( {CE} \right)\end{array}\)
\(\begin{array}{l}\frac{{EA}}{{EC}} = \frac{3}{1} = 3\\\frac{{AE}}{{AC}} = \frac{3}{4} = 0,75\\\frac{{CE}}{{CA}} = \frac{1}{4} = 0,25\end{array}\)
3. Dựa vào tỉ số của các cặp ta thấy các cặp có tỉ số bằng nhau:
\(\begin{array}{l}\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}} = \frac{3}{1} = 3\\\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{3}{4} = 0,75\\\frac{{BD}}{{BA}} = \frac{{CE}}{{CA}} = \frac{1}{4} = 0,25\end{array}\)
Để chia đoạn thẳng \(AB\) thành năm phần bằng nhau, An làm như sau (Hình 6.10):
1. Vẽ đường thẳng \(d\) di qua \(A\) không trùng với \(AB.\) Trên \(d\) lấy năm điểm \(C,D,E,F,G\) sao cho \(AC = CD = DE = {\rm{EF = FG;}}\)
2. Vẽ các đường thẳng đi qua \(C,D,E,F\) song song với đường thẳng \(BG\) và cắt \(AB\) lần lượt tại \(C',D',E',F'.\)
Khi đó, các điểm này chia \(AB\) thành năm đoạn thẳng bằng nhau. Em hãy giải thích vì sao?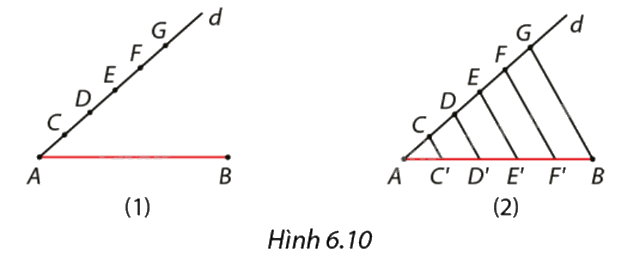
Phương pháp giải:
Dựa vào định lý Thales để chứng minh:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Vì đường thẳng đi qua \(C,D,E,F\) song song với đường thẳng \(BG\) và cắt \(AB\) lần lượt tại \(C',D',E',F'.\) Áp dụng định lý Thales thuận ta có:
\(\begin{array}{l}CC'//DD'\\ = > \frac{{CA}}{{CD}} = \frac{{C'A}}{{C'D'}}\end{array}\)
Mà \(\begin{array}{l}CA = CD\\ = > C'A = C'D'\end{array}\)
Chứng minh tương tự với \(DD'//EE',EE'//FF',FF'//BG\)
Ta có: \(AC' = C'D' = D'E' = E'F' = F'B'\).
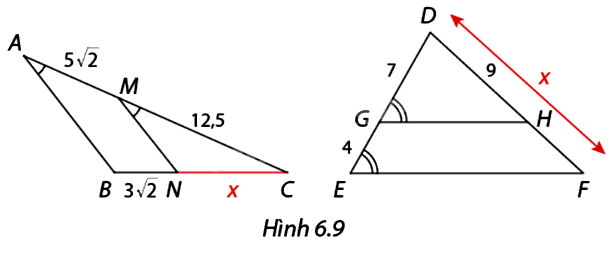
Tính độ dài \(x\) trong mỗi trường hợp ở Hình 6.9.
Phương pháp giải:
Dựa vào Định lý Thales thuận và tỉ số của hai đoạn thẳng để tính độ dài x.
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
Lời giải chi tiết:
Xét tam giác \(ABC\), ta có:
\(\begin{array}{l}\frac{{MA}}{{MC}} = \frac{{NB}}{{NC}}\\ \Leftrightarrow \frac{{5\sqrt 2 }}{{12,5}} = \frac{{3\sqrt 2 }}{x}\\ \Leftrightarrow x = 7,5\end{array}\)
Xét tam giác \(DEF\), ta có:
\(\begin{array}{l}\frac{{DG}}{{DE}} = \frac{{DH}}{{DF}}\\ \Leftrightarrow \frac{7}{{11}} = \frac{9}{x}\\ \Leftrightarrow x = \frac{{99}}{7}\end{array}\)
Giấy vở học sinh có các đường kẻ song song và cách đều nhau. Khi vẽ một đường thẳng bất kì cắt các đường kẻ, ta được các đoạn thẳng liên tiếp bằng nhau (Hình 6.5a). Xét \(\Delta ABC\) trong hình 6.5b.
1. Chọn \(BD\) làm đơn vị đo độ dài, em hãy tính độ dài \(AD,AB\) và các tỉ số \(\frac{{DA}}{{DB}},\frac{{AD}}{{AB}},\frac{{BD}}{{BA}}.\)
2. Chọn \(CE\) làm đơn vị đo độ dài, em hãy tính độ dài \(AE,AC\) và các tỉ số \(\frac{{EA}}{{EC}},\frac{{AE}}{{AC}},\frac{{CE}}{{CA}}.\)
3. So sánh các cặp tỉ số\(\frac{{DA}}{{DB}}\) và \(\frac{{EA}}{{EC}},\frac{{AD}}{{AB}}\) và \(\frac{{AE}}{{AC}},\frac{{BD}}{{BA}}\) và \(\frac{{CE}}{{CA}}.\) Em có nhận xét gì về các cặp đoạn thẳng được cho?
Phương pháp giải:
Tỉ số của hai đoạn thẳng AB và CD là tỉ số độ dài của chúng theo cùng một đơn vị đo, kí hiệu \(\frac{{AB}}{{CD}}\).
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
Lời giải chi tiết:
1. Chọn \(BD\) là đơn vị đo độ dài, ta có:
\(AD = 3\left( {BD} \right)\)
\(AB = 4\left( {BD} \right)\)
\(\begin{array}{l}\frac{{DA}}{{DB}} = \frac{3}{1} = 3\\\frac{{AD}}{{AB}} = \frac{3}{4} = 0,75\\\frac{{BD}}{{BA}} = \frac{1}{4} = 0,25\end{array}\)
2. Chọn \(CE\) làm đơn vị đo độ dài, ta có:
\(\begin{array}{l}AE = 3\left( {CE} \right)\\AC = 4\left( {CE} \right)\end{array}\)
\(\begin{array}{l}\frac{{EA}}{{EC}} = \frac{3}{1} = 3\\\frac{{AE}}{{AC}} = \frac{3}{4} = 0,75\\\frac{{CE}}{{CA}} = \frac{1}{4} = 0,25\end{array}\)
3. Dựa vào tỉ số của các cặp ta thấy các cặp có tỉ số bằng nhau:
\(\begin{array}{l}\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}} = \frac{3}{1} = 3\\\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{3}{4} = 0,75\\\frac{{BD}}{{BA}} = \frac{{CE}}{{CA}} = \frac{1}{4} = 0,25\end{array}\)
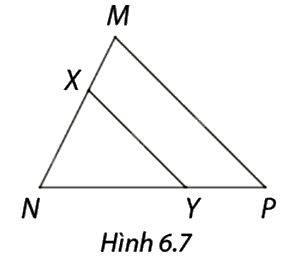
Trong hình 6.7, \(XY\) song song với \(MP.\) Em hãy cho biết tên đoạn thẳng ở các ô?.
\(\frac{{MX}}{{NX}} = \frac{?}{?};\frac{{NY}}{?} = \frac{?}{{MN}}.\)
Phương pháp giải:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
\(\begin{array}{l}\frac{{MX}}{{NX}} = \frac{{PY}}{{NY}};\\\frac{{NY}}{{NP}} = \frac{{NX}}{{MN}}\end{array}\)
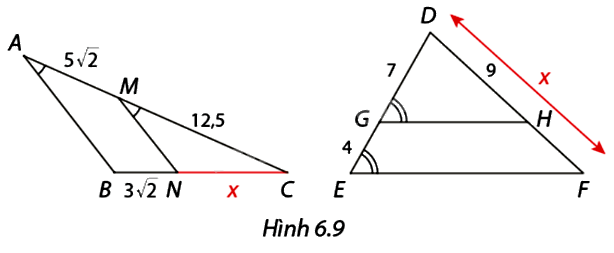
Tính độ dài \(x\) trong mỗi trường hợp ở Hình 6.9.
Phương pháp giải:
Dựa vào Định lý Thales thuận và tỉ số của hai đoạn thẳng để tính độ dài x.
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
Lời giải chi tiết:
Xét tam giác \(ABC\), ta có:
\(\begin{array}{l}\frac{{MA}}{{MC}} = \frac{{NB}}{{NC}}\\ \Leftrightarrow \frac{{5\sqrt 2 }}{{12,5}} = \frac{{3\sqrt 2 }}{x}\\ \Leftrightarrow x = 7,5\end{array}\)
Xét tam giác \(DEF\), ta có:
\(\begin{array}{l}\frac{{DG}}{{DE}} = \frac{{DH}}{{DF}}\\ \Leftrightarrow \frac{7}{{11}} = \frac{9}{x}\\ \Leftrightarrow x = \frac{{99}}{7}\end{array}\)
Để chia đoạn thẳng \(AB\) thành năm phần bằng nhau, An làm như sau (Hình 6.10):
1. Vẽ đường thẳng \(d\) di qua \(A\) không trùng với \(AB.\) Trên \(d\) lấy năm điểm \(C,D,E,F,G\) sao cho \(AC = CD = DE = {\rm{EF = FG;}}\)
2. Vẽ các đường thẳng đi qua \(C,D,E,F\) song song với đường thẳng \(BG\) và cắt \(AB\) lần lượt tại \(C',D',E',F'.\)
Khi đó, các điểm này chia \(AB\) thành năm đoạn thẳng bằng nhau. Em hãy giải thích vì sao?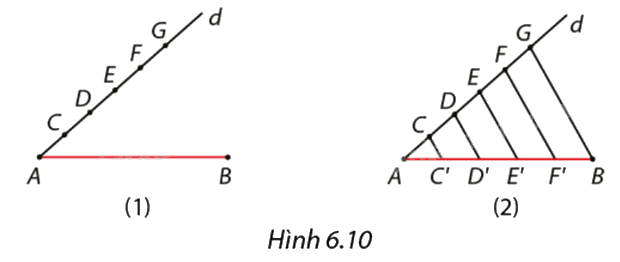
Phương pháp giải:
Dựa vào định lý Thales để chứng minh:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Vì đường thẳng đi qua \(C,D,E,F\) song song với đường thẳng \(BG\) và cắt \(AB\) lần lượt tại \(C',D',E',F'.\) Áp dụng định lý Thales thuận ta có:
\(\begin{array}{l}CC'//DD'\\ = > \frac{{CA}}{{CD}} = \frac{{C'A}}{{C'D'}}\end{array}\)
Mà \(\begin{array}{l}CA = CD\\ = > C'A = C'D'\end{array}\)
Chứng minh tương tự với \(DD'//EE',EE'//FF',FF'//BG\)
Ta có: \(AC' = C'D' = D'E' = E'F' = F'B'\).
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi, hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của chúng là vô cùng quan trọng để giải quyết các bài tập liên quan.
Mục 2 thường bao gồm các nội dung sau:
Để giải các bài tập trong mục này, các em cần:
Bài tập: Cho hình chữ nhật ABCD, AB = 8cm, BC = 6cm. Tính độ dài đường chéo AC.
Giải:
Vì ABCD là hình chữ nhật nên góc ABC vuông. Áp dụng định lý Pitago vào tam giác ABC, ta có:
AC2 = AB2 + BC2 = 82 + 62 = 64 + 36 = 100
Suy ra AC = √100 = 10cm.
Khi giải các bài tập về tứ giác, các em cần chú ý:
Ngoài SGK Toán 8, các em có thể tham khảo thêm các tài liệu sau:
Để học tốt môn Toán 8, các em cần:
Hy vọng với những hướng dẫn chi tiết trên, các em sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 38, 39, 40 SGK Toán 8. Chúc các em học tập tốt!