Chào mừng các em học sinh lớp 8 đến với bài giải chi tiết mục 5 trang 5, 6 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và giải quyết các bài tập một cách hiệu quả.
Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để các em hiểu sâu sắc về nội dung bài học.
Dựa vào tính chất phân phối
Tìm tổng và hiệu của hai đơn thức \(6{x^3}y\)và \(11{x^3}y\).
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng thực hiện phép tính, tính tổng và hiệu của hai đơn thức.
Lời giải chi tiết:
Ta có:
\(6{x^3}y + 11{x^3}y = \left( {6 + 11} \right){x^3}y = 17{x^3}y\)
\(6{x^3}y - 11{x^3}y = \left( {6 - 11} \right){x^3}y = - 5{x^3}y\)
Dựa vào tính chất phân phối của phép nhân đối với phép cộng các số, hãy thực hiện các phép tính sau và viết kết quả dưới dạng đơn thức thu gọn.
a) \(2{x^2}y + 7{x^2}y\);
b) \(6x{y^3} - 9x{y^3}\).
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng thực hiện phép tính.
Thu gọn các kết quả vừa tìm được
Lời giải chi tiết:
a) \(2{x^2}y + 7{x^2}y = \left( {2 + 7} \right){x^2}y = 9{x^2}y\)
b) \(6x{y^3} - 9x{y^3} = \left( {6 - 9} \right)x{y^3} = - 3x{y^3}\).
Dựa vào tính chất phân phối của phép nhân đối với phép cộng các số, hãy thực hiện các phép tính sau và viết kết quả dưới dạng đơn thức thu gọn.
a) \(2{x^2}y + 7{x^2}y\);
b) \(6x{y^3} - 9x{y^3}\).
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng thực hiện phép tính.
Thu gọn các kết quả vừa tìm được
Lời giải chi tiết:
a) \(2{x^2}y + 7{x^2}y = \left( {2 + 7} \right){x^2}y = 9{x^2}y\)
b) \(6x{y^3} - 9x{y^3} = \left( {6 - 9} \right)x{y^3} = - 3x{y^3}\).
Tìm tổng và hiệu của hai đơn thức \(6{x^3}y\)và \(11{x^3}y\).
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng thực hiện phép tính, tính tổng và hiệu của hai đơn thức.
Lời giải chi tiết:
Ta có:
\(6{x^3}y + 11{x^3}y = \left( {6 + 11} \right){x^3}y = 17{x^3}y\)
\(6{x^3}y - 11{x^3}y = \left( {6 - 11} \right){x^3}y = - 5{x^3}y\)
Tìm diện tích của phần được tô màu trong Hình 1.2 và Hình 1.3 theo \(a\)và \(b\).
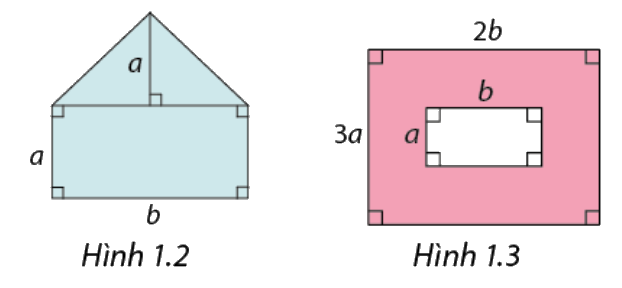
Phương pháp giải:
Hình 1.2: Sử dụng công thức tính diện tích hình tam giác và hình chữ nhật để tính diện tích phân tô màu theo \(a\)và \(b\)
Hình 1.3. Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích phân tô màu theo \(a\)và \(b\).
Lời giải chi tiết:
Hình 1.2: Diện tích phần tô màu là tổng diện tích hình tam giác có chiều cao là \(a\), cạnh đáy là \(b\)và diện tích hình chữ nhật có chiều dài và chiều rộng lần lượt là \(b;a\).
Vậy diện tích phần tô màu hình 1.2 là:\(\frac{1}{2}ab + ab = \left( {\frac{1}{2} + 1} \right)ab = \frac{3}{2}ab\)
Hình 1.3: Diện tích phần tô màu là hiệu của hai hình chữ nhật.
Vậy diện tích phần tô màu hình 1.3 là: \(3a.2b - a.b = 6ab - ab = 5ab\)
Tìm diện tích của phần được tô màu trong Hình 1.2 và Hình 1.3 theo \(a\)và \(b\).
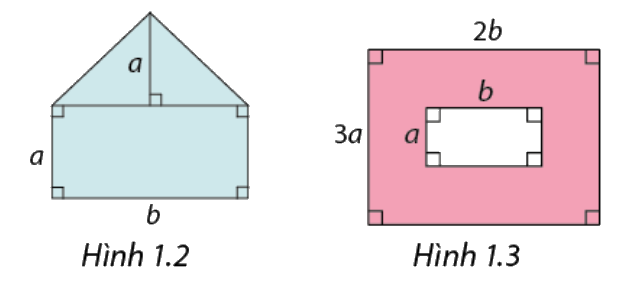
Phương pháp giải:
Hình 1.2: Sử dụng công thức tính diện tích hình tam giác và hình chữ nhật để tính diện tích phân tô màu theo \(a\)và \(b\)
Hình 1.3. Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích phân tô màu theo \(a\)và \(b\).
Lời giải chi tiết:
Hình 1.2: Diện tích phần tô màu là tổng diện tích hình tam giác có chiều cao là \(a\), cạnh đáy là \(b\)và diện tích hình chữ nhật có chiều dài và chiều rộng lần lượt là \(b;a\).
Vậy diện tích phần tô màu hình 1.2 là:\(\frac{1}{2}ab + ab = \left( {\frac{1}{2} + 1} \right)ab = \frac{3}{2}ab\)
Hình 1.3: Diện tích phần tô màu là hiệu của hai hình chữ nhật.
Vậy diện tích phần tô màu hình 1.3 là: \(3a.2b - a.b = 6ab - ab = 5ab\)
Mục 5 trong SGK Toán 8 trang 5 và 6 thường tập trung vào một chủ đề cụ thể, ví dụ như các phép biến đổi đại số đơn giản, giải phương trình bậc nhất một ẩn, hoặc các bài toán liên quan đến đa thức. Việc nắm vững kiến thức nền tảng và áp dụng đúng các phương pháp giải là chìa khóa để giải quyết thành công các bài tập trong mục này.
Bài 1 thường yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia đa thức. Để giải bài này, các em cần nhớ các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các công thức rút gọn đa thức.
Bài 2 thường yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Để giải bài này, các em cần nhớ các bước giải phương trình:
Bài 3 thường là một bài toán thực tế yêu cầu học sinh vận dụng kiến thức đã học để giải quyết. Để giải bài này, các em cần:
Để giải bài tập Toán 8 một cách hiệu quả, các em cần lưu ý những điều sau:
Ví dụ 1: Giải phương trình 2x + 5 = 11
Giải:
Vậy nghiệm của phương trình là x = 3.
Hy vọng với bài giải chi tiết và những lưu ý quan trọng trên, các em học sinh lớp 8 sẽ tự tin hơn khi giải các bài tập trong mục 5 trang 5, 6 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao!