Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Ở bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 1 trang 59, 60, 61 sách giáo khoa Toán 8. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Ta đã được học về tứ giác.
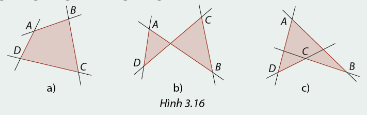
Trong trường hợp nào ở Hình 3.16, tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Phương pháp giải:
Xét từng hình xem hình nào tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Lời giải chi tiết:
Ta thấy hình a) có tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Còn hình b) và hình c) không có tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Vẽ ba điểm A, B, C không thẳng hàng bất kì. Hãy vẽ thêm điểm D và E sao cho tứ giác ABCD lồi còn tứ giác ABCE không lồi.
Phương pháp giải:
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của nó.
Đầu tiên vẽ A, B, C không thẳng hàng bất kì, sau đó vẽ thêm điểm D và E sao cho tứ giác ABCD lồi còn tứ giác ABCE không lồi.
Lời giải chi tiết:
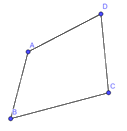
Tứ giác ABCD lồi
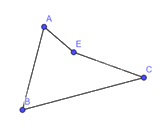
Tứ giác ABCE không lồi
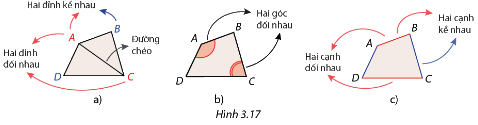
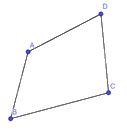
Viết tên tất cả các cặp cạnh kề nhau, cặp cạnh đối nhau, cặp đỉnh kề nhau, cặp đỉnh đối nhau còn lại của tứ giác \(ABCD\) trong Hình 3.17.
Phương pháp giải:
Hai đỉnh thuộc cùng một cạnh được gọi là hai đỉnh kề nhau, hai đỉnh không thuộc cùng một cạnh được gọi là hải đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau gọi là đường chéo.
Hai góc tại hai đỉnh đối nhau của tứ giác gọi là hai góc đối nhau.
Hai cạnh có cùng đầu mút gọi là hai cạnh kề nhau, hai cạnh không có chung đầu mút gọi là hai cạnh đối nhau.
Lời giải chi tiết:
Cặp cạnh kề nhau: \(AB,AD\);\(DA,DC\);\(CD,CB\);\(BA,BC\).
Cặp cạnh đối nhau: \(AB,DC;AB,BC\).
Cặp đỉnh kề nhau: \(A,C;B,D;C,A\).
Ta đã được học về tứ giác. Em hãy cho biết trong trường hợp nào của Hình 3.14, bốn đoạn thẳng AB, BC và AD tạo thành một tứ giác.
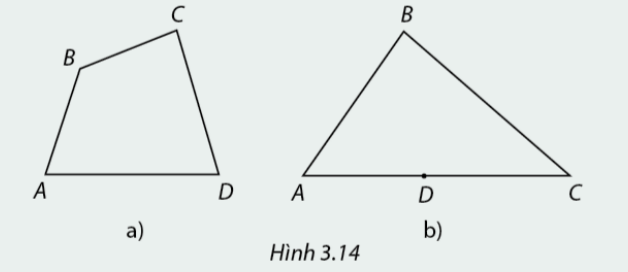
Phương pháp giải:
Tứ giác \(ABCD\) là hình gồm bốn đoạn thẳng \(AB,BC,CD\) và \(DA\), trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Lời giải chi tiết:
Hình a) có bốn đoạn thẳng \(AB,BC,CD\) và \(DA\) tạo thành một tứ giác, còn hình b) không phải hình tứ giác vì bốn đoạn thẳng \(AB,BC,CD\) và \(DA\) ở hình b) có \(AD,DC\) cùng nằm trên một đường thẳng.
Ta đã được học về tứ giác. Em hãy cho biết trong trường hợp nào của Hình 3.14, bốn đoạn thẳng AB, BC và AD tạo thành một tứ giác.
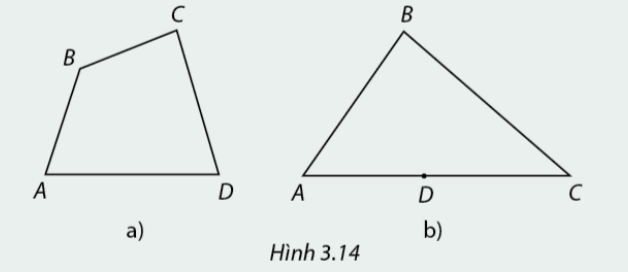
Phương pháp giải:
Tứ giác \(ABCD\) là hình gồm bốn đoạn thẳng \(AB,BC,CD\) và \(DA\), trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Lời giải chi tiết:
Hình a) có bốn đoạn thẳng \(AB,BC,CD\) và \(DA\) tạo thành một tứ giác, còn hình b) không phải hình tứ giác vì bốn đoạn thẳng \(AB,BC,CD\) và \(DA\) ở hình b) có \(AD,DC\) cùng nằm trên một đường thẳng.
Trong trường hợp nào ở Hình 3.16, tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
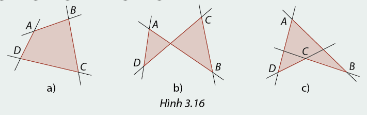
Phương pháp giải:
Xét từng hình xem hình nào tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Lời giải chi tiết:
Ta thấy hình a) có tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Còn hình b) và hình c) không có tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Vẽ ba điểm A, B, C không thẳng hàng bất kì. Hãy vẽ thêm điểm D và E sao cho tứ giác ABCD lồi còn tứ giác ABCE không lồi.
Phương pháp giải:
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của nó.
Đầu tiên vẽ A, B, C không thẳng hàng bất kì, sau đó vẽ thêm điểm D và E sao cho tứ giác ABCD lồi còn tứ giác ABCE không lồi.
Lời giải chi tiết:
Tứ giác ABCD lồi
Tứ giác ABCE không lồi
Viết tên tất cả các cặp cạnh kề nhau, cặp cạnh đối nhau, cặp đỉnh kề nhau, cặp đỉnh đối nhau còn lại của tứ giác \(ABCD\) trong Hình 3.17.
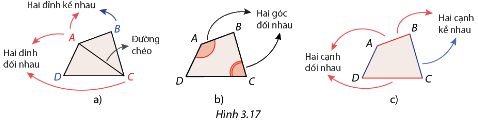
Phương pháp giải:
Hai đỉnh thuộc cùng một cạnh được gọi là hai đỉnh kề nhau, hai đỉnh không thuộc cùng một cạnh được gọi là hải đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau gọi là đường chéo.
Hai góc tại hai đỉnh đối nhau của tứ giác gọi là hai góc đối nhau.
Hai cạnh có cùng đầu mút gọi là hai cạnh kề nhau, hai cạnh không có chung đầu mút gọi là hai cạnh đối nhau.
Lời giải chi tiết:
Cặp cạnh kề nhau: \(AB,AD\);\(DA,DC\);\(CD,CB\);\(BA,BC\).
Cặp cạnh đối nhau: \(AB,DC;AB,BC\).
Cặp đỉnh kề nhau: \(A,C;B,D;C,A\).
Mục 1 của chương trình Toán 8 thường tập trung vào việc ôn tập và hệ thống hóa các kiến thức cơ bản về đa thức, phân thức đại số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài tập phức tạp hơn trong chương trình.
Mục 1 thường bao gồm các nội dung sau:
Bài 1: Thực hiện các phép tính sau:
Giải:
Bài 2: Phân tích các đa thức sau thành nhân tử:
Giải:
Bài 3: Rút gọn các biểu thức sau:
Giải:
Để học Toán 8 hiệu quả, các em nên:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập trong mục 1 trang 59, 60, 61 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao!