Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi xin giới thiệu bộ giải chi tiết các bài tập trong mục 1 trang 6, 7, 8 sách giáo khoa Toán 8, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp lời giải chính xác, dễ hiểu, đi kèm với phương pháp giải khoa học.
Nhiệt độ
Viết công thức tính diện tích \(y\left( {c{m^2}} \right)\) của hình vuông có độ dài cạnh đáy bằng x (cm). Ứng với mỗi giá trị của x, tìm được bao nhiêu giá trị tương ứng của y?
Phương pháp giải:
Áp dụng công thức tính diện tích hình vuông để xác định mỗi giá trị của x thì tìm được bao nhiêu giá trị của y.
Lời giải chi tiết:
Diện tích của hình vuông đó là:
\(y = x.x\left( {c{m^2}} \right)\)
Vậy ta thấy với mỗi giá trị của x thì chỉ tìm được 1 giá trị của y.
Số tiền y (nghìn đồng) khách hàng phải thanh toán khi di chuyển quãng đường x (km) bằng taxi của hãng A cho bởi công thức \(y = f\left( x \right) = 13x + 10\).
a) Đại lượng y có là hàm số của đại lượng x không?
b) Tính \(f\left( 5 \right)\). Giá trị này cho biết điều gì?
Phương pháp giải:
Xác định xem mỗi giá trị của x ta có luôn xác định được chỉ một giá trị tương ứng của y không bằng cách thay giá trị x bất kì vào y nếu giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì đại lượng y chính là hàm số của đại lượng x.
Thay \(x = 5\) vào công thức \(y = f\left( x \right) = 13x + 10\). Sau đó cho biết giá trị y.
Lời giải chi tiết:
a) Ta có công thức: \(y = f\left( x \right) = 13x + 10\).
Với \(x = 1\) thì \(y = 23\)
Với \(x = 2\) thì \(y = 26\)
Với \(x = 3\) thì \(y = 49\)
Vậy ta thấy với mỗi giá trị của x thì ta luôn xác định được chỉ một giá trị tương ứng y nên y được gọi là hàm số của x và x là biến của y.
b) Thay \(x = 5\) vào công thức \(y = f\left( x \right) = 13x + 10\). Ta có:
\(\begin{array}{l}y = 13.5 + 10\\ = > y = 75\end{array}\)
Với giá trị này cho ta biết số tiền mà khách hàng phải thanh toán khi di chuyển quãng đường 5 km bằng xe taxi của hãng A là 75 nghìn đồng.
Nhiệt độ \(T\left( {^\circ C} \right)\) tại các thời điểm t (giờ) trong ngày 16/10/2022 tại Thành phố Hồ Chí Minh được cho trong Bảng 5.2.

a) Hãy cho biết nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ, 10 giờ, 16 giờ ngày 16/10/2022.
b) Với mỗi giá trị của t có bao nhiêu giá trị tương ứng của T.
Phương pháp giải:
Quan sát Bảng 5.2 và xác định nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ, 10 giờ, 16 giờ ngày 16/10/2022.
Lời giải chi tiết:
a) Quan sát Bảng 5.2 ta thấy nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ là 230C, lúc 10 giờ là 280C, lúc 16 giờ là 320C.
b) Với mỗi giá trị của t chỉ có 1 giá trị tương ứng của T.
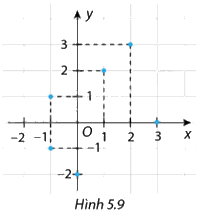
Quan hệ giữa hai đại lượng \(x,y\) được biểu diễn bởi sáu điểm cho trên mặt phẳng tọa độ ở Hình 5.9.
a) Tìm số thích hợp cho ô trống trong Bảng 5.6, với \(\left( {x;y} \right)\) là tọa độ của các điểm đã cho

b) Đại lượng y có là hàm số của đại lượng x không?
Phương pháp giải:
Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ để điền vào Bảng 5.6.
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y.
Lời giải chi tiết:
a) Dựa vào các tọa độ trong Hình 5.9, ta có Bảng 5.6 như sau:

b) Quan sát Bảng 5.6 ta thấy mỗi giá trị của x luôn luôn xác định được chỉ một giá trị tương ứng của y nên y được gọi là hàm số của x và x được gọi là biến số.
Trong hộp đồ chơi lắp ráp có năm mảnh hình chữ nhật khác nhau. Diện tích \(S\left( {c{m^2}} \right)\) và chiều rộng r (cm) của các mảnh hình chữ nhật được thống kê trong Bảng 5.3.
a) Tìm chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\)
b) Tìm chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\)
c) Quan hệ giữa S và r có thỏa mãn điều kiện “cứ mỗi giá trị của S có đúng một giá trị của r” không?

Phương pháp giải:
Dựa vào dữ liệu trong Bảng 5.3 và công thức tính diện tích hình chữ nhật để tìm chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\) và chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\), sau đó đưa ra nhận xét về các giá trị.
Lời giải chi tiết:
a) Quan sát Bảng 5.3 ta thấy chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\) là \(r = 1\left( {cm} \right)\)
b) Quan sát Bảng 5.3 ta thấy chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\) là \(r = 2\left( {cm} \right)\)
c) Qua đó ta thấy cứ mỗi một giá trị của S thì cho ra đúng một giá trị của r.
Nhiệt độ \(T\left( {^\circ C} \right)\) tại các thời điểm t (giờ) trong ngày 16/10/2022 tại Thành phố Hồ Chí Minh được cho trong Bảng 5.2.

a) Hãy cho biết nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ, 10 giờ, 16 giờ ngày 16/10/2022.
b) Với mỗi giá trị của t có bao nhiêu giá trị tương ứng của T.
Phương pháp giải:
Quan sát Bảng 5.2 và xác định nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ, 10 giờ, 16 giờ ngày 16/10/2022.
Lời giải chi tiết:
a) Quan sát Bảng 5.2 ta thấy nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ là 230C, lúc 10 giờ là 280C, lúc 16 giờ là 320C.
b) Với mỗi giá trị của t chỉ có 1 giá trị tương ứng của T.
Viết công thức tính diện tích \(y\left( {c{m^2}} \right)\) của hình vuông có độ dài cạnh đáy bằng x (cm). Ứng với mỗi giá trị của x, tìm được bao nhiêu giá trị tương ứng của y?
Phương pháp giải:
Áp dụng công thức tính diện tích hình vuông để xác định mỗi giá trị của x thì tìm được bao nhiêu giá trị của y.
Lời giải chi tiết:
Diện tích của hình vuông đó là:
\(y = x.x\left( {c{m^2}} \right)\)
Vậy ta thấy với mỗi giá trị của x thì chỉ tìm được 1 giá trị của y.
Trong hộp đồ chơi lắp ráp có năm mảnh hình chữ nhật khác nhau. Diện tích \(S\left( {c{m^2}} \right)\) và chiều rộng r (cm) của các mảnh hình chữ nhật được thống kê trong Bảng 5.3.
a) Tìm chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\)
b) Tìm chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\)
c) Quan hệ giữa S và r có thỏa mãn điều kiện “cứ mỗi giá trị của S có đúng một giá trị của r” không?

Phương pháp giải:
Dựa vào dữ liệu trong Bảng 5.3 và công thức tính diện tích hình chữ nhật để tìm chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\) và chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\), sau đó đưa ra nhận xét về các giá trị.
Lời giải chi tiết:
a) Quan sát Bảng 5.3 ta thấy chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\) là \(r = 1\left( {cm} \right)\)
b) Quan sát Bảng 5.3 ta thấy chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\) là \(r = 2\left( {cm} \right)\)
c) Qua đó ta thấy cứ mỗi một giá trị của S thì cho ra đúng một giá trị của r.
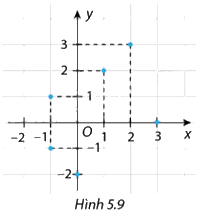
Quan hệ giữa hai đại lượng \(x,y\) được biểu diễn bởi sáu điểm cho trên mặt phẳng tọa độ ở Hình 5.9.
a) Tìm số thích hợp cho ô trống trong Bảng 5.6, với \(\left( {x;y} \right)\) là tọa độ của các điểm đã cho

b) Đại lượng y có là hàm số của đại lượng x không?
Phương pháp giải:
Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ để điền vào Bảng 5.6.
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y.
Lời giải chi tiết:
a) Dựa vào các tọa độ trong Hình 5.9, ta có Bảng 5.6 như sau:

b) Quan sát Bảng 5.6 ta thấy mỗi giá trị của x luôn luôn xác định được chỉ một giá trị tương ứng của y nên y được gọi là hàm số của x và x được gọi là biến số.
Số tiền y (nghìn đồng) khách hàng phải thanh toán khi di chuyển quãng đường x (km) bằng taxi của hãng A cho bởi công thức \(y = f\left( x \right) = 13x + 10\).
a) Đại lượng y có là hàm số của đại lượng x không?
b) Tính \(f\left( 5 \right)\). Giá trị này cho biết điều gì?
Phương pháp giải:
Xác định xem mỗi giá trị của x ta có luôn xác định được chỉ một giá trị tương ứng của y không bằng cách thay giá trị x bất kì vào y nếu giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì đại lượng y chính là hàm số của đại lượng x.
Thay \(x = 5\) vào công thức \(y = f\left( x \right) = 13x + 10\). Sau đó cho biết giá trị y.
Lời giải chi tiết:
a) Ta có công thức: \(y = f\left( x \right) = 13x + 10\).
Với \(x = 1\) thì \(y = 23\)
Với \(x = 2\) thì \(y = 26\)
Với \(x = 3\) thì \(y = 49\)
Vậy ta thấy với mỗi giá trị của x thì ta luôn xác định được chỉ một giá trị tương ứng y nên y được gọi là hàm số của x và x là biến của y.
b) Thay \(x = 5\) vào công thức \(y = f\left( x \right) = 13x + 10\). Ta có:
\(\begin{array}{l}y = 13.5 + 10\\ = > y = 75\end{array}\)
Với giá trị này cho ta biết số tiền mà khách hàng phải thanh toán khi di chuyển quãng đường 5 km bằng xe taxi của hãng A là 75 nghìn đồng.
Mục 1 của chương trình Toán 8 thường tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản, các biểu thức đại số đơn giản, và các khái niệm về số thực. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo. Bài tập trong mục này thường bao gồm các dạng bài tập như:
Trang 6 SGK Toán 8 thường chứa các bài tập về việc ôn tập các phép toán với số nguyên, số hữu tỉ. Các bài tập này giúp học sinh củng cố kiến thức về thứ tự thực hiện các phép toán, quy tắc dấu ngoặc, và các tính chất giao hoán, kết hợp, phân phối.
Ví dụ, bài tập 1 trang 6 có thể yêu cầu tính giá trị của biểu thức: (12 + 36) : 4 - 5. Để giải bài tập này, ta thực hiện các bước sau:
12 + 36 = 4848 : 4 = 1212 - 5 = 7Trang 7 SGK Toán 8 thường chứa các bài tập về việc rút gọn biểu thức đại số. Các bài tập này giúp học sinh rèn luyện kỹ năng sử dụng các tính chất của phép toán để biến đổi biểu thức về dạng đơn giản nhất.
Ví dụ, bài tập 2 trang 7 có thể yêu cầu rút gọn biểu thức: 3x + 5y - 2x + y. Để giải bài tập này, ta thực hiện các bước sau:
(3x - 2x) + (5y + y)x + 6yTrang 8 SGK Toán 8 thường chứa các bài tập về việc giải phương trình đơn giản. Các bài tập này giúp học sinh làm quen với các bước giải phương trình và rèn luyện kỹ năng tìm nghiệm của phương trình.
Ví dụ, bài tập 3 trang 8 có thể yêu cầu giải phương trình: 2x + 5 = 11. Để giải bài tập này, ta thực hiện các bước sau:
2x = 11 - 52x = 6x = 6 : 2Để giải bài tập Toán 8 hiệu quả, các em cần:
Giaitoan.edu.vn là địa chỉ học toán online uy tín, cung cấp đầy đủ các bài giải chi tiết, dễ hiểu, cùng với các bài giảng video sinh động, giúp các em học toán hiệu quả hơn. Chúng tôi luôn cập nhật kiến thức mới nhất và đáp ứng nhu cầu học tập của học sinh.
| Dạng bài tập | Ví dụ |
|---|---|
| Tính giá trị biểu thức | (15 - 9) * 2 + 5 |
| Rút gọn biểu thức | 4x + 2y - x + 3y |
| Giải phương trình | 3x - 7 = 5 |