Chào mừng bạn đến với bài học về Lý thuyết Đa thức nhiều biến, một phần quan trọng trong chương trình Toán 8. Bài học này được thiết kế để giúp bạn hiểu rõ các khái niệm cơ bản, tính chất và ứng dụng của đa thức nhiều biến.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn tự tin chinh phục môn Toán.
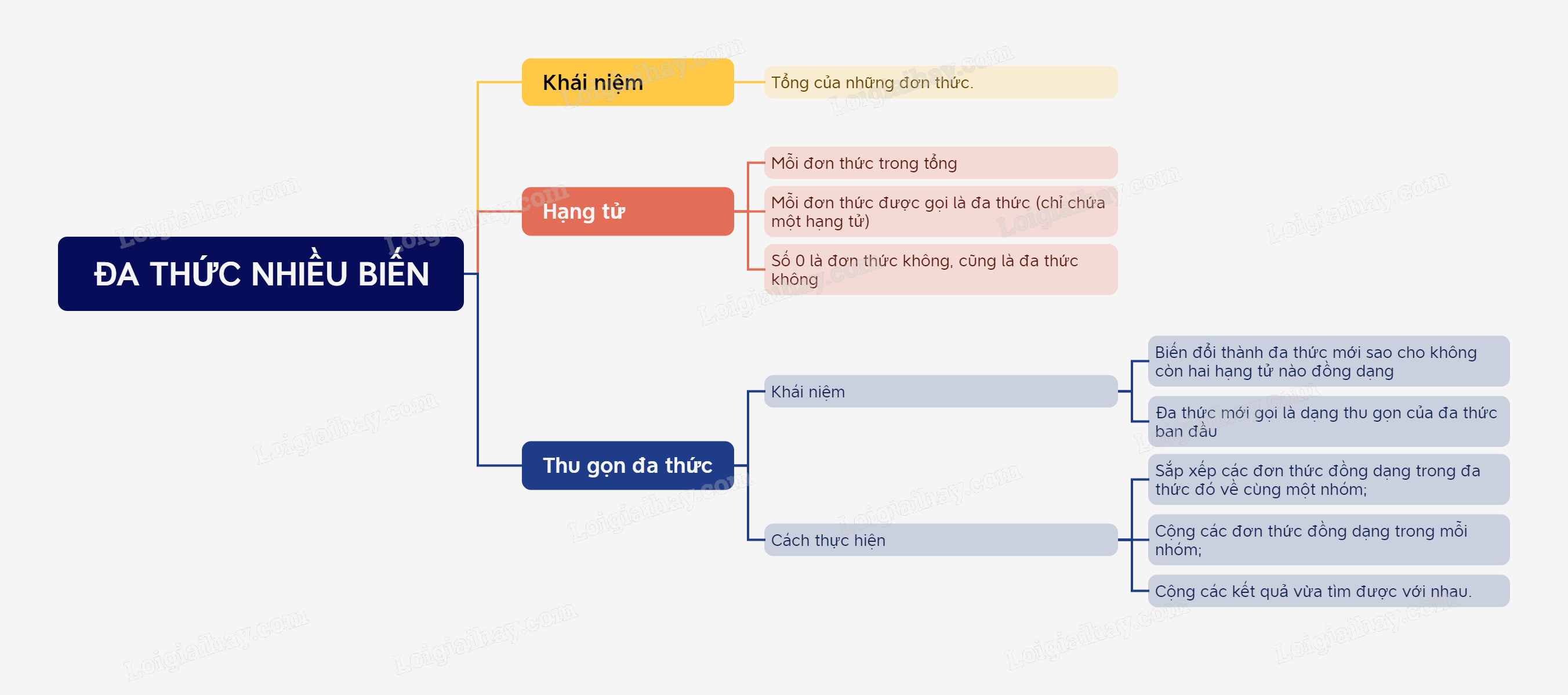
Đa thức là gì?
1. Khái niệm
- Đa thức là một tổng của những đơn thức.
- Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).
Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.
Ví dụ:
\({x^2} - 4x + 3;{x^2}\; + {\rm{ }}3xy{z^2}\; - {\rm{ }}yz{\rm{ }} + {\rm{ }}1;\left( {x{\rm{ }} + {\rm{ }}3y} \right){\rm{ }} + \left( {2x{\rm{ }}--{\rm{ }}y} \right)\) là đa thức.
\(\frac{{x + y}}{{x - y}},\frac{{{x^2} + 2}}{{{x^2} - {y^2}}}\) không phải là đa thức.
\({x^2} - 4x + 3\)có 3 hạng tử \({x^2}; - 4x;3\).
\({x^2}\; + {\rm{ }}3xy{z^2}\; - {\rm{ }}yz{\rm{ }} + {\rm{ }}1\) có 4 hạng tử \({x^2}{\rm{; }}3xy{z^2};\; - {\rm{ }}yz{\rm{ ; }}1\).
2. Thu gọn đa thức
- Thu gọn đa thức P là viết đa thức này thành đa thức Q sao cho trong đa thức Q không còn hai hạng tử nào đồng dạng. Đa thức Q gọi là dạng thu gọn của đa thức P.
- Cách thu gọn đa thức
Để thu gọn một đa thức, ta làm như sau:
+ Sắp xếp các đơn thức đồng dạng trong đa thức đó về cùng một nhóm;
+ Cộng các đơn thức đồng dạng trong mỗi nhóm;
+ Cộng các kết quả vừa tìm được với nhau.
Ví dụ:
\(\begin{array}{l}A = {x^3} - 2{x^2}y - {x^2}y + 3x{y^2} - {y^3}\\\,\,\,\,\, = {x^3} - 3{x^2}y - 3x{y^2} - {y^3}\end{array}\)
Đa thức nhiều biến là một biểu thức đại số bao gồm các số, các biến và các phép toán cộng, trừ, nhân, chia (với số khác 0) giữa chúng. Trong chương trình Toán 8, việc nắm vững lý thuyết về đa thức nhiều biến là vô cùng quan trọng, không chỉ để giải các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Một đa thức nhiều biến là một biểu thức đại số có dạng:
P(x1, x2, ..., xn) = A + Bx1 + Cx2 + ... + Dxn + Ex1x2 + ... + Fxn-1xn + ...
Trong đó:
Bậc của một đa thức nhiều biến là tổng số mũ của tất cả các biến trong mỗi hạng tử của đa thức. Ví dụ:
Nếu đa thức không có biến nào thì bậc của đa thức bằng 0.
Để cộng hoặc trừ hai đa thức, ta thực hiện cộng hoặc trừ các hạng tử đồng dạng. Hạng tử đồng dạng là các hạng tử có cùng phần biến và cùng bậc.
Ví dụ: (2x2y + 3xy2) + (x2y - xy2) = 3x2y + 2xy2
Để nhân hai đa thức, ta sử dụng tính chất phân phối của phép nhân đối với phép cộng. Tức là, ta nhân mỗi hạng tử của đa thức thứ nhất với mỗi hạng tử của đa thức thứ hai, sau đó cộng tất cả các kết quả lại.
Ví dụ: (x + y)(x - y) = x2 - y2
Bài tập này yêu cầu học sinh xác định bậc của một đa thức cho trước. Để làm được bài tập này, học sinh cần nắm vững khái niệm về bậc của đa thức và cách tính bậc của đa thức.
Bài tập này yêu cầu học sinh thu gọn một đa thức cho trước bằng cách cộng các hạng tử đồng dạng. Để làm được bài tập này, học sinh cần nắm vững khái niệm về hạng tử đồng dạng và cách cộng các hạng tử đồng dạng.
Bài tập này yêu cầu học sinh tính giá trị của một đa thức tại một giá trị cụ thể của các biến. Để làm được bài tập này, học sinh cần thay các giá trị của các biến vào đa thức và thực hiện các phép tính.
Đa thức nhiều biến có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để nắm vững lý thuyết về đa thức nhiều biến, bạn nên luyện tập thường xuyên các bài tập trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tham gia các khóa học trực tuyến hoặc tìm kiếm sự giúp đỡ của giáo viên, bạn bè.
Lý thuyết Đa thức nhiều biến là một phần quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết này sẽ giúp bạn tự tin giải các bài tập và ứng dụng kiến thức vào thực tế. Chúc bạn học tập tốt!