Chào mừng các em học sinh đến với bài giải chi tiết bài 6.30 trang 65 SGK Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em chinh phục môn Toán một cách tự tin và đạt kết quả cao.
Cho tam giác \(ABC\) có hai đường cao
Đề bài
Cho tam giác \(ABC\) có hai đường cao $BD$ và $CE$ cắt nhau tại O. Chứng minh rẳng:
a) Tam giác \(ABD\) đồng dạng với tam giác
b) \(OE.OC = OB.OD\)\(ACE\)
Phương pháp giải - Xem chi tiết
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết
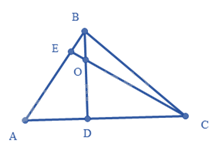
a) Xét tam giác \(ABD\) và tam giác \(ACE\), ta có:
\(\widehat A\) là góc chung
\(\widehat {ADB} = \widehat {AEC} = 90^\circ \)
=> \(\Delta ABD\)∽\(\Delta ACE\) (góc vuông-góc nhọn)
b) Xét tam giác \(OEB\) và tam giác \(ODC\), ta có:
\(\widehat {OEB} = \widehat {ODC} = 90^\circ \)
\(\widehat {EOB} = \widehat {DOC}\) (2 góc đối đỉnh)
=> \(\Delta OEB\)∽\(\Delta ODC\) (góc vuông-góc nhọn)
Ta có tỉ lệ đồng dạng:
\(\begin{array}{l}\frac{{OE}}{{OD}} = \frac{{OB}}{{OC}}\\ \Leftrightarrow OE.OC = OB.OD(dpcm)\end{array}\)
Bài 6.30 trang 65 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần nắm vững các tính chất của hình chữ nhật, đặc biệt là mối quan hệ giữa các cạnh đối và các góc đối.
Đề bài yêu cầu chúng ta chứng minh một biểu thức đại số liên quan đến các cạnh của hình chữ nhật. Để làm được điều này, chúng ta cần phân tích kỹ đề bài, xác định các yếu tố đã cho và các yếu tố cần chứng minh. Việc vẽ hình minh họa sẽ giúp chúng ta hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
Đề bài: Cho hình chữ nhật ABCD. Gọi E là trung điểm của cạnh AD. Gọi F là trung điểm của cạnh BC. Chứng minh rằng AE = BF.
Lời giải:
Bước 1: Chúng ta dựa vào tính chất cơ bản của hình chữ nhật để khẳng định rằng độ dài cạnh AD bằng độ dài cạnh BC. Đây là nền tảng để chúng ta thực hiện các bước tiếp theo.
Bước 2 và 3: Vì E và F là trung điểm của các cạnh AD và BC, chúng ta sử dụng định nghĩa trung điểm để biểu diễn độ dài AE và BF theo độ dài của các cạnh AD và BC.
Bước 4: Cuối cùng, chúng ta kết hợp các kết quả từ các bước trước để chứng minh rằng AE bằng BF. Đây là kết luận của bài toán.
Bài toán này có thể được mở rộng bằng cách thay đổi vị trí của các điểm E và F, hoặc bằng cách yêu cầu chứng minh các mối quan hệ khác giữa các đoạn thẳng trong hình chữ nhật. Ví dụ, chúng ta có thể yêu cầu chứng minh rằng DE = CF.
Khi giải bài tập về hình chữ nhật, học sinh cần:
Bài 6.30 trang 65 SGK Toán 8 là một bài toán cơ bản về hình chữ nhật, giúp học sinh rèn luyện kỹ năng vận dụng các tính chất của hình chữ nhật để giải quyết các bài toán đơn giản. Hy vọng rằng với lời giải chi tiết và các giải thích rõ ràng, các em học sinh đã hiểu rõ cách giải bài toán này.
| Tính chất | Mô tả |
|---|---|
| Các cạnh đối song song | AB // CD và AD // BC |
| Các cạnh đối bằng nhau | AB = CD và AD = BC |
| Các góc đều bằng 90 độ | ∠A = ∠B = ∠C = ∠D = 90° |
| Hai đường chéo bằng nhau | AC = BD |
| Hai đường chéo cắt nhau tại trung điểm của mỗi đường | O là trung điểm của AC và BD |