Chào mừng các em học sinh đến với bài giải chi tiết bài 3.44 trang 90 SGK Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
Chứng minh rằng:
Đề bài
Chứng minh rằng:
a) Trong một hình bình hành (không là hình thoi), các tia phân giác của các góc cắt nhau tạo thành một hình chữ nhật.
b) Trong một hình chữ nhật (không là hình vuông), các tia phân giác của các góc cắt nhau tạo thành một hình vuông.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hình bình hành, hình chữ nhật hình vuông để chứng minh.
Lời giải chi tiết
a) Ta có hình bình hành \(ABCD\):
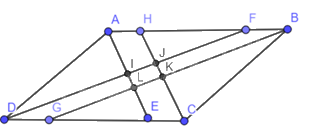
Ta có \(\widehat {EAB} = \widehat {AED}\) ( sole trong)
Lại có \(\widehat {EAB} = \widehat {HCD}\) (đường phân giác của hai góc đối trong hình bình hành)
→ \(\widehat {AED} = \widehat {HCD}\)
→ \(AE//HC\)
→ \(IL//JK\) (1)
Có \(\widehat {FDC} = \widehat {ABG}\) (đường phân giác của hai góc đối trong hình bình hành)
Mà \(\widehat {ABG} = \widehat {BGC}\) (sole trong)
→ \(DF//BG\)
→ \(IJ//LK\) (2)
Từ (1) và (2) suy ra \(IJKL\) là hình bình hành
Ta có \(\widehat {AED} = \widehat {EAB}\)
Mà \(\widehat {EAB} + \widehat {CDF} = 90^\circ \) (phân giác của hai góc kề trong hình bình hành)
→ \(\widehat {AED} = \widehat {CDF} = 90^\circ \)
→ \(\widehat {DIE} = 90^\circ \)
→ \(\widehat {JIL} = 90^\circ \)
→ \(IJKL\) là hình chữ nhật.
b) Cho hình chữ nhật \(ABCD\):
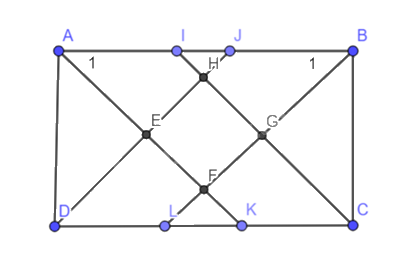
\(ABCD\) là hình chữ nhật \( = > \widehat A = \widehat B = 90^\circ \)
\(AF,BF\) lần lượt là phân giác của \(\widehat A,\widehat B = > \widehat {BAF} = \widehat {ABF} = \frac{1}{2}\widehat A = \frac{1}{2}\widehat B = \frac{1}{2}90^\circ = 45^\circ \)
Xét tam giác \(ABF\) có: \(\widehat {BAF} + \widehat {ABF} + \widehat {AFB} = 180^\circ \)
\(\begin{array}{l}2\widehat {BAF} + \widehat {AFB} = 180^\circ \\ = > \widehat {AFB} = 180^\circ - 2\widehat {BAF} = 180^\circ - 2.45^\circ = 90^\circ \end{array}\)
Chứng minh tương tự, ta có \(\widehat {DHC} = 90^\circ ,\widehat {AED} = 90^\circ \)
Tứ giác \(EFGH\) có \(\widehat {AFB} = 90^\circ ,\widehat {DHC} = 90^\circ ,\widehat {AED} = 90^\circ \) nên \(EFGH\) là hình chữ nhật.
Xét \(\Delta ADE\) và \(\Delta BCG\) có:
\(\begin{array}{l}\widehat {ADE} = \widehat {GCB} = 45^\circ \\AD = BC\\\widehat {DAE} = \widehat {CBG} = 45^\circ \\ = > \Delta ADE = \Delta BCG\left( {g - c - g} \right)\\ = > AE = BG\end{array}\)
\(\Delta ABF\) cân ở \(F\) (vì \(\widehat {BAF} = \widehat {ABF} = 45^\circ \)) =>\(AF = BF\)
Ta có:
\(\left\{ \begin{array}{l}AF = AE + EF\\BF = BG + GF\end{array} \right.\) mà \(\left\{ \begin{array}{l}AE = BG\\AF = BF\end{array} \right.\), suy ra \(EF = GF\)
Hình chữ nhật \(EFGH\) có \(EF = GF\) nên \(EFGH\) là hình vuông
Bài 3.44 trang 90 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hình chữ nhật, bao gồm:
Bài toán 3.44 thường yêu cầu học sinh chứng minh một tứ giác là hình chữ nhật dựa trên các điều kiện cho trước. Để làm được điều này, học sinh cần phân tích kỹ đề bài, xác định các yếu tố đã cho và lựa chọn dấu hiệu nhận biết hình chữ nhật phù hợp.
Dưới đây là hướng dẫn giải chi tiết bài 3.44 trang 90 SGK Toán 8. Lưu ý rằng, tùy thuộc vào từng đề bài cụ thể, phương pháp giải có thể khác nhau. Tuy nhiên, các bước cơ bản sau đây sẽ giúp học sinh tiếp cận và giải quyết bài toán một cách hiệu quả:
Đề bài: Cho tứ giác ABCD có AB = CD, AD = BC. Chứng minh rằng ABCD là hình chữ nhật.
Giải:
Để nắm vững kiến thức về hình chữ nhật và rèn luyện kỹ năng giải bài tập, học sinh nên thực hành giải thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, học sinh có thể tham gia các diễn đàn học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn cùng lớp.
Bài 3.44 trang 90 SGK Toán 8 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình chữ nhật và rèn luyện kỹ năng giải bài tập hình học. Hy vọng rằng, với hướng dẫn chi tiết và ví dụ minh họa trên đây, các em học sinh sẽ tự tin giải quyết bài toán này một cách hiệu quả.
| Khái niệm | Định nghĩa |
|---|---|
| Hình chữ nhật | Hình có bốn góc vuông |
| Tính chất | Các cạnh đối song song và bằng nhau, các góc đối bằng nhau, đường chéo cắt nhau tại trung điểm của mỗi đường và bằng nhau. |