Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách giáo khoa Toán 8. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Với mục tiêu hỗ trợ học sinh học tập hiệu quả, chúng tôi đã biên soạn bộ giải đáp án trang 46, 47 SGK Toán 8 một cách cẩn thận và đầy đủ.
Hãy cùng khám phá và chinh phục những bài toán Toán 8 một cách tự tin!
1. Cắt tam giác \(ABC\) bất kì có \(AB = 2AC.\) Gấp giấy sao cho cạnh \(AC\) chồng lên
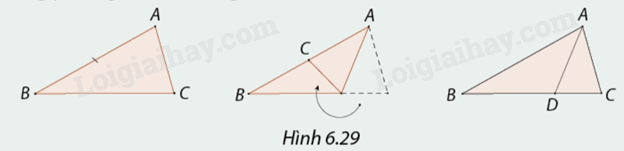
1. Cắt tam giác \(ABC\) bất kì có \(AB = 2AC.\) Gấp giấy sao cho cạnh \(AC\) chồng lên cạnh \(AB\) để xác định đường phân giác \(AD\) (Hình 6.29). Đo độ dài các đoạn thẳng \(BD,CD.\) Tính và so sánh tỉ số \(\frac{{BD}}{{CD}}\) và \(\frac{{AB}}{{AC}}.\)
2. Thực hiện tương tự với trường hợp \(\frac{{AB}}{{AC}} = \frac{3}{2}.\) Em có nhận xét gì về vị trí chân đường phân giác của tam giác?
Phương pháp giải:
Đo độ dài các đoạn thẳng \(BD,CD.\) Sau đó tính và so sánh tỉ số \(\frac{{BD}}{{CD}}\) và \(\frac{{AB}}{{AC}}\) dựa vào tỉ lệ của hai đoạn thẳng.
Lời giải chi tiết:
1. Gọi số đo AC là 1 thì số đo AB là 2.
Đo độ dài đoạn thẳng \(BD = 2;CD = 1\)
Tỉ số \(\frac{{BD}}{{CD}} = \frac{2}{1} = 2\)
Tỉ số \(\frac{{AB}}{{AC}} = \frac{2}{1} = 2\)
Ta thấy \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = 2\) .
2. Với \(AB = 3;AC = 2\) thì số đo độ dài đoạn thẳng \(BD = 3;CD = 2\)
Ta thấy tỉ số \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = \frac{3}{2}\)
Từ hai trường hợp trên, ta thấy dựa vào độ dài cạnh ta xác định được vị trí chân đường phân giác của một tam giác.
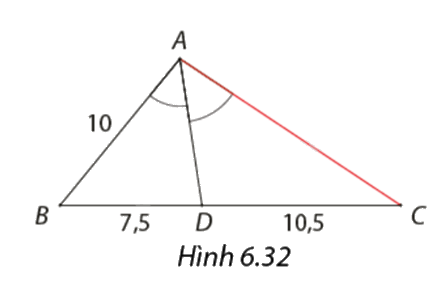
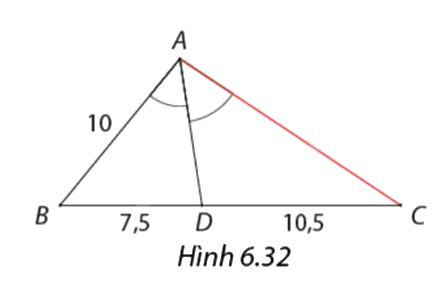
Tìm độ dài cạnh \(AC\) trong Hình 6.32.
Phương pháp giải:
Dựa vào tính chất đường phân giác của một tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải chi tiết:
Xét tam giác \(ABC\) , ta có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
=> AD là đường phân giác
Áp dụng tính chất đường phân giác ta có:
\(\frac{{BA}}{{AC}} = \frac{{BD}}{{DC}} \Leftrightarrow \frac{{10}}{{AC}} = \frac{{7,5}}{{10,5}} \Rightarrow AC = 14\)
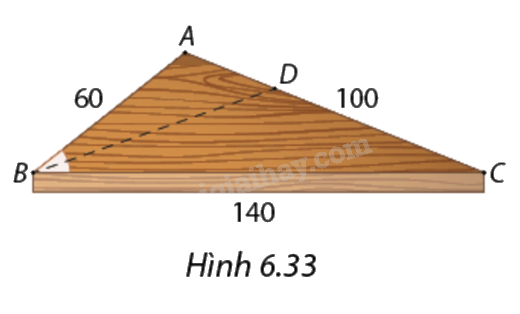
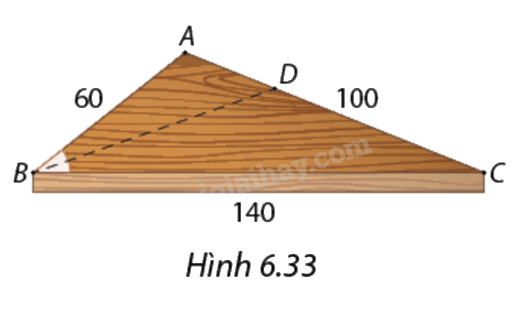
Bác thợ mộc cần cưa mảnh ván hình tam giác \(ABC\) thành hai phần theo đường phân giác \(BD\) của góc \(B\) (Hình 6.33), nhưng bác chỉ có thước đo độ dài. Bác đo được \(AB = 60\,cm,AC = 100cm\) và \(BC = 140cm.\) Hãy giúp bác xác định vị trí điểm \(D\) và vẽ đường cưa.
Phương pháp giải:
Dựa vào tính chất đường phân giác của một tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải chi tiết:
Áp dụng tính chất đường phân giác ta có:
\(\frac{{AD}}{{DC}} = \frac{{BA}}{{BC}} \Leftrightarrow \frac{x}{{100 - x}} = \frac{{60}}{{140}} \Leftrightarrow \frac{x}{{100 - x}} = \frac{3}{7} \Leftrightarrow 7x = 300 - 3x \Rightarrow x = 30\)
Vậy \(AD = 30;DC = 100 - 30 = 70\)
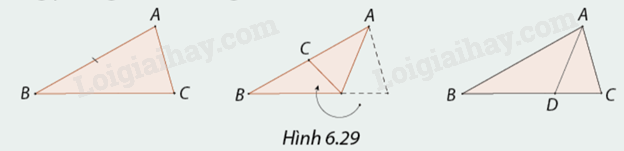
1. Cắt tam giác \(ABC\) bất kì có \(AB = 2AC.\) Gấp giấy sao cho cạnh \(AC\) chồng lên cạnh \(AB\) để xác định đường phân giác \(AD\) (Hình 6.29). Đo độ dài các đoạn thẳng \(BD,CD.\) Tính và so sánh tỉ số \(\frac{{BD}}{{CD}}\) và \(\frac{{AB}}{{AC}}.\)
2. Thực hiện tương tự với trường hợp \(\frac{{AB}}{{AC}} = \frac{3}{2}.\) Em có nhận xét gì về vị trí chân đường phân giác của tam giác?
Phương pháp giải:
Đo độ dài các đoạn thẳng \(BD,CD.\) Sau đó tính và so sánh tỉ số \(\frac{{BD}}{{CD}}\) và \(\frac{{AB}}{{AC}}\) dựa vào tỉ lệ của hai đoạn thẳng.
Lời giải chi tiết:
1. Gọi số đo AC là 1 thì số đo AB là 2.
Đo độ dài đoạn thẳng \(BD = 2;CD = 1\)
Tỉ số \(\frac{{BD}}{{CD}} = \frac{2}{1} = 2\)
Tỉ số \(\frac{{AB}}{{AC}} = \frac{2}{1} = 2\)
Ta thấy \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = 2\) .
2. Với \(AB = 3;AC = 2\) thì số đo độ dài đoạn thẳng \(BD = 3;CD = 2\)
Ta thấy tỉ số \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = \frac{3}{2}\)
Từ hai trường hợp trên, ta thấy dựa vào độ dài cạnh ta xác định được vị trí chân đường phân giác của một tam giác.
Tìm độ dài cạnh \(AC\) trong Hình 6.32.
Phương pháp giải:
Dựa vào tính chất đường phân giác của một tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải chi tiết:
Xét tam giác \(ABC\) , ta có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
=> AD là đường phân giác
Áp dụng tính chất đường phân giác ta có:
\(\frac{{BA}}{{AC}} = \frac{{BD}}{{DC}} \Leftrightarrow \frac{{10}}{{AC}} = \frac{{7,5}}{{10,5}} \Rightarrow AC = 14\)
Bác thợ mộc cần cưa mảnh ván hình tam giác \(ABC\) thành hai phần theo đường phân giác \(BD\) của góc \(B\) (Hình 6.33), nhưng bác chỉ có thước đo độ dài. Bác đo được \(AB = 60\,cm,AC = 100cm\) và \(BC = 140cm.\) Hãy giúp bác xác định vị trí điểm \(D\) và vẽ đường cưa.
Phương pháp giải:
Dựa vào tính chất đường phân giác của một tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải chi tiết:
Áp dụng tính chất đường phân giác ta có:
\(\frac{{AD}}{{DC}} = \frac{{BA}}{{BC}} \Leftrightarrow \frac{x}{{100 - x}} = \frac{{60}}{{140}} \Leftrightarrow \frac{x}{{100 - x}} = \frac{3}{7} \Leftrightarrow 7x = 300 - 3x \Rightarrow x = 30\)
Vậy \(AD = 30;DC = 100 - 30 = 70\)
Sách giáo khoa Toán 8 trang 46 và 47 tập trung vào các dạng bài tập liên quan đến hình học, cụ thể là các kiến thức về tứ giác. Các bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để chứng minh, tính toán và giải quyết các vấn đề thực tế.
Bài 1 thường yêu cầu học sinh xác định các yếu tố của tứ giác (bốn cạnh, bốn góc) và phân loại tứ giác dựa trên các tính chất đặc biệt (hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông). Để giải bài tập này, học sinh cần nắm vững định nghĩa và các tính chất của từng loại tứ giác.
Bài 2 tập trung vào hình thang cân, một loại tứ giác đặc biệt có hai cạnh đáy song song và hai cạnh bên bằng nhau. Các bài tập thường yêu cầu học sinh chứng minh một tứ giác là hình thang cân, tính độ dài các cạnh, đường cao hoặc góc của hình thang cân.
Bài 3 giới thiệu về đường trung bình của tam giác và hình thang. Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh, song song với cạnh còn lại và bằng một nửa độ dài cạnh đó. Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên, song song với hai đáy và bằng trung bình cộng độ dài hai đáy. Các bài tập thường yêu cầu học sinh tính độ dài đường trung bình hoặc vận dụng tính chất của đường trung bình để giải quyết các vấn đề liên quan.
Bài 4 là bài tập vận dụng, yêu cầu học sinh sử dụng kiến thức về đường trung bình để giải quyết các bài toán thực tế, ví dụ như tính độ dài các đoạn thẳng, chứng minh các điểm thẳng hàng hoặc các đường thẳng song song.
Bài tập: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính chiều cao của hình thang.
Giải:
Để học tốt môn Toán 8, bạn cần:
Hy vọng với bộ giải đáp án chi tiết và phương pháp giải bài tập hiệu quả, bạn sẽ tự tin hơn khi học Toán 8. Chúc bạn học tập tốt và đạt kết quả cao!