Chào mừng các em học sinh đến với bài giải bài 6.4 trang 42 SGK Toán 8 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ các em học tập tốt hơn. Hãy cùng bắt đầu với bài giải bài 6.4 trang 42 Toán 8 ngay bây giờ!
Viết tên các đường thẳng song song trong Hình 6.16.
Đề bài
Viết tên các đường thẳng song song trong Hình 6.16.
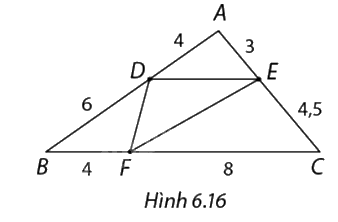
Phương pháp giải - Xem chi tiết
Dựa vào định lí Thales đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
Dựa vào định lí Thales đảo, ta có:
\(\begin{array}{l}\frac{{DA}}{{DB}} = \frac{4}{6} = \frac{2}{3}\\\frac{{EA}}{{EC}} = \frac{3}{{4,5}} = \frac{2}{3}\\ = > \frac{{DA}}{{DB}} = \frac{{EA}}{{EC}} = \frac{2}{3}\end{array}\)
Bài 6.4 trang 42 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần nắm vững các tính chất của hình chữ nhật, đặc biệt là tính chất về các cạnh đối song song và bằng nhau, các góc vuông, và đường chéo bằng nhau.
Bài tập 6.4 yêu cầu học sinh chứng minh một tứ giác là hình chữ nhật dựa trên các điều kiện cho trước. Thông thường, các điều kiện này liên quan đến việc chứng minh các góc vuông, các cạnh đối song song và bằng nhau, hoặc đường chéo bằng nhau. Việc lựa chọn phương pháp chứng minh phù hợp là yếu tố quan trọng để giải quyết bài toán một cách hiệu quả.
Để giải bài 6.4 trang 42 SGK Toán 8, chúng ta có thể áp dụng một trong các phương pháp sau:
Đề bài: Cho tứ giác ABCD có AB = CD, AD = BC. Chứng minh rằng ABCD là hình chữ nhật.
Lời giải:
Xét tam giác ABD và tam giác CDB, ta có:
Do đó, tam giác ABD = tam giác CDB (cạnh - cạnh - cạnh). Suy ra ∠ABD = ∠CDB và ∠ADB = ∠CBD.
Vì ∠ABD = ∠CDB, nên AB // CD (hai góc so le trong bằng nhau). Tương tự, vì ∠ADB = ∠CBD, nên AD // BC (hai góc so le trong bằng nhau).
Vậy, tứ giác ABCD là hình bình hành (vì có các cặp cạnh đối song song).
Ta có AB = CD (giả thiết). Trong hình bình hành, các cạnh đối bằng nhau. Do đó, AB = CD và AD = BC.
Vì ABCD là hình bình hành có một góc vuông (ví dụ, ∠A = 90°), nên ABCD là hình chữ nhật.
Để củng cố kiến thức về hình chữ nhật và rèn luyện kỹ năng giải toán, các em có thể luyện tập thêm các bài tập sau:
Khi giải các bài tập về hình chữ nhật, các em nên:
Bài 6.4 trang 42 SGK Toán 8 là một bài tập quan trọng giúp các em hiểu sâu hơn về hình chữ nhật và các tính chất của nó. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!