Chào mừng bạn đến với bài học về Lý thuyết Tính chất cơ bản của phân thức đại số, một phần quan trọng trong chương trình Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp kiến thức nền tảng vững chắc, giúp bạn tự tin giải quyết các bài toán liên quan.
Bài học này sẽ trình bày chi tiết các tính chất cơ bản, ví dụ minh họa và bài tập thực hành, giúp bạn hiểu rõ và áp dụng thành thạo kiến thức vào giải bài tập.
Phân thức có tính chất gì?
1. Tính chất cơ bản của phân thức
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
\(\frac{A}{B} = \frac{{A.M}}{{B.M}}\) (M là một đa thức khác đa thức không).
Nếu chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
\(\frac{A}{B} = \frac{{A:N}}{{B:N}}\) (N là một đa thức nhân tử chung).
Ví dụ: Để biến đổi phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) thành \(\frac{{ - 1}}{{x + y}}\), ta chia cả tử và mẫu của phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) cho y – x, khi đó \(\frac{{x - y}}{{{y^2} - {x^2}}} = \frac{{ - (y - x)}}{{(y - x)(y + x)}} = \frac{{ - 1}}{{x + y}}\)
2. Rút gọn phân thức
Để rút gọn một phân thức, ta thực hiện như sau:
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung (trong một số trường hợp, cần đổi dấu của tử hoặc mẫu để nhận ra nhân tử chung);
- Chia cả tử và mẫu cho nhân tử chung.
Lưu ý: Tại giá trị của các biến thỏa mãn điều kiện xác định của một phân thức, giá trị của phân thức đó và của phân thức sau khi rút gọn là như nhau.
Ví dụ: Rút gọn phân thức \(\frac{{{x^3} - 6{x^2} + 9x}}{{{x^2} - 9x}}\) ta được:
\(\frac{{{x^3} - 6{x^2} + 9x}}{{{x^3} - 9x}} = \frac{{x({x^2} - 6x + 9)}}{{x(x - 3)(x + 3)}} = \frac{{x{{\left( {x - 3} \right)}^2}}}{{x(x - 3)(x + 3)}} = \frac{{x - 3}}{{x + 3}}\)
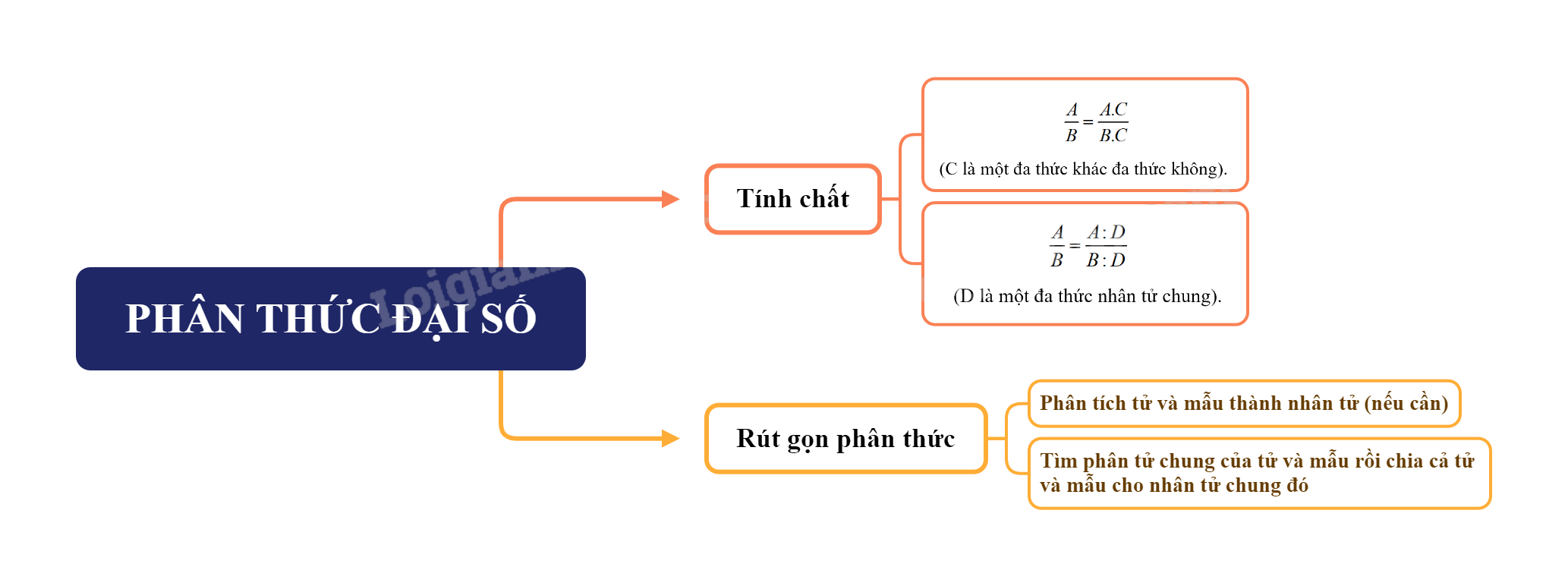
Phân thức đại số là một khái niệm quan trọng trong đại số, đặc biệt là ở chương trình Toán 8. Việc nắm vững lý thuyết và các tính chất cơ bản của phân thức đại số là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về chủ đề này, dựa trên nội dung sách giáo khoa Toán 8.
Một phân thức đại số là một biểu thức có dạng P/Q, trong đó P và Q là các đa thức, và Q khác 0. P được gọi là tử số, Q được gọi là mẫu số.
Phân thức P/Q xác định khi và chỉ khi mẫu số Q khác 0. Điều này có nghĩa là chúng ta cần tìm các giá trị của biến sao cho Q ≠ 0.
Tính chất cơ bản của phân thức đại số tương tự như tính chất cơ bản của phân số. Cụ thể:
Tính chất 1: Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác 0 thì phân thức mới bằng phân thức ban đầu. P/Q = (P.M)/(Q.M), với M là một đa thức khác 0.
Tính chất 2: Nếu chia cả tử và mẫu của một phân thức với cùng một đa thức khác 0 thì phân thức mới bằng phân thức ban đầu. P/Q = (P:M)/(Q:M), với M là một đa thức khác 0.
Rút gọn phân thức đại số là việc tìm một phân thức tương đương đơn giản hơn. Để rút gọn phân thức, ta thực hiện các bước sau:
Quy đồng mẫu thức của các phân thức đại số là việc tìm các phân thức tương đương có cùng mẫu thức. Để quy đồng mẫu thức, ta thực hiện các bước sau:
Các phép toán cộng, trừ, nhân, chia phân thức đại số được thực hiện tương tự như các phép toán trên phân số, nhưng cần chú ý đến điều kiện xác định của phân thức.
Cộng, trừ phân thức:P/Q + R/S = (P.S + R.Q)/(Q.S) và P/Q - R/S = (P.S - R.Q)/(Q.S)
Nhân phân thức:P/Q . R/S = (P.R)/(Q.S)
Chia phân thức:P/Q : R/S = (P.S)/(Q.R)
Ví dụ 1: Rút gọn phân thức (x2 - 1)/(x + 1)
Giải: Ta có (x2 - 1)/(x + 1) = ((x - 1)(x + 1))/(x + 1) = x - 1 (với x ≠ -1)
Ví dụ 2: Quy đồng mẫu thức của các phân thức 1/x và 1/(x + 1)
Giải: Mẫu thức chung nhỏ nhất là x(x + 1). Ta có 1/x = (x + 1)/(x(x + 1)) và 1/(x + 1) = x/(x(x + 1))
Lý thuyết Tính chất cơ bản của phân thức đại số là một phần quan trọng trong chương trình Toán 8. Việc nắm vững các khái niệm, tính chất và quy tắc sẽ giúp bạn tự tin giải quyết các bài toán liên quan đến phân thức đại số. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán.