Lý Thuyết Hệ Số Góc Đường Thẳng y = ax + b (a ≠ 0)

Lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0), Đường thẳng song song và đường thẳng cắt nhau SGK Toán 8 - Cùng khám phá

Lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Chào mừng bạn đến với bài học về lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0) trong chương trình Toán 8. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hệ số góc, cũng như cách ứng dụng nó để xác định mối quan hệ giữa các đường thẳng.

Chúng ta sẽ cùng nhau khám phá định nghĩa, ý nghĩa của hệ số góc, cách xác định hệ số góc của một đường thẳng, và đặc biệt là mối liên hệ giữa hệ số góc với tính song song và cắt nhau của các đường thẳng.

Hệ số góc của đường thẳng là gì?

1. Hệ số góc của đường thẳng y = ax + b (a\( \ne \)0)

Cho đường thẳng d: y = ax + b (a\( \ne \)0). M là giao điểm của d với trục hoành, N là điểm thuộc d có tung đô dương. Ta gọi \(\widehat {xMN} = \alpha \) là góc tạo bởi đường thẳng d với trục Ox.

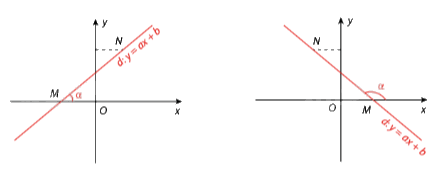
Lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0), Đường thẳng song song và đường thẳng cắt nhau SGK Toán 8 - Cùng khám phá 1

Tổng quát:

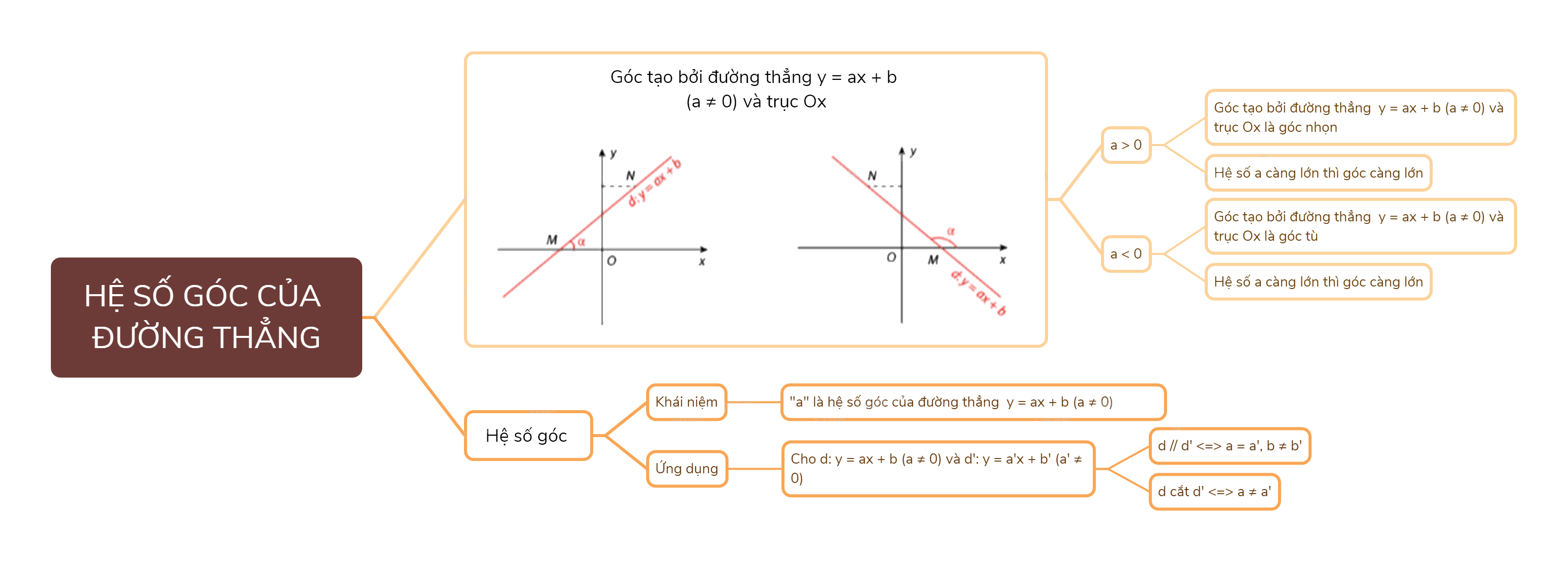
Khi a > 0 thì góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc \(\alpha \) càng lớn.

Khi a < 0 thì góc tạo bởi đường thẳng y = ax + b (a\( \ne \)0) và trục Ox là góc tù. Hệ số a càng lớn thì góc \(\alpha \) càng lớn.

Định nghĩa:

Hệ số a được gọi là hệ số góc của đường thẳng y = ax + b (hay là hệ số góc của đồ thị hàm số y = ax + b (a \( \ne \) 0)

Ví dụ: Đường thẳng y = 3x – 1 có hệ số góc là 3;

y = 2 – x có hệ số góc là -1.

2. Đường thẳng song song

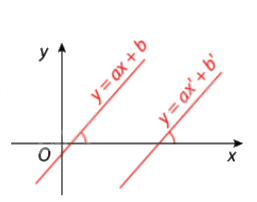
Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) song song với nhau khi a = a’; b \( \ne \) b’ và ngược lại.

3. Đường thẳng cắt nhau

Hai đường thẳng y = ax + b (a\( \ne \)0) và y = a’x + b’ (a’\( \ne \)0) cắt nhau khi a \( \ne \) a’ và ngược lại.

Ví dụ:

Đường thẳng y = -x + 1 và đường thẳng y = -x song song với nhau vì a = a’ = -1, b = 1 \( \ne \) 0 = b’.

Đường thẳng y = -x + 1 và đường thẳng y = 2x + 1 cắt nhau vì a = -1 \( \ne \)2 = a’.

Lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0), Đường thẳng song song và đường thẳng cắt nhau SGK Toán 8 - Cùng khám phá 3

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0), Đường thẳng song song và đường thẳng cắt nhau SGK Toán 8 - Cùng khám phá đặc sắc thuộc chuyên mục toán 8 trên đề thi toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0) - Toán 8

Trong mặt phẳng tọa độ, đường thẳng có phương trình tổng quát là ax + by + c = 0. Tuy nhiên, để nghiên cứu về tính chất hình học của đường thẳng, ta thường xét phương trình đường thẳng dưới dạng y = ax + b (a ≠ 0). Trong đó, 'a' được gọi là hệ số góc của đường thẳng.

1. Định nghĩa Hệ số góc

Hệ số góc của đường thẳng y = ax + b (a ≠ 0) là giá trị của 'a'. Nó thể hiện độ dốc của đường thẳng so với trục hoành. Hệ số góc có thể dương, âm hoặc bằng không (trong trường hợp đường thẳng song song với trục hoành).

2. Ý nghĩa của Hệ số góc

a > 0: Đường thẳng đi lên khi x tăng (đường thẳng dốc lên).
a < 0: Đường thẳng đi xuống khi x tăng (đường thẳng dốc xuống).
a = 0: Đường thẳng song song với trục hoành (đường thẳng nằm ngang).

Góc α tạo bởi đường thẳng y = ax + b với trục hoành được tính bởi công thức: tan α = a. Do đó, hệ số góc 'a' chính là tan của góc tạo bởi đường thẳng và trục hoành.

3. Xác định Hệ số góc của đường thẳng

Để xác định hệ số góc của một đường thẳng, ta có thể:

Nếu đường thẳng có phương trình y = ax + b: Hệ số góc là 'a'.
Nếu đường thẳng có phương trình ax + by + c = 0: Đưa phương trình về dạng y = ax + b, sau đó xác định 'a'.
Nếu biết hai điểm thuộc đường thẳng: Gọi hai điểm đó là M(x₁, y₁) và N(x₂, y₂). Hệ số góc được tính bởi công thức: a = (y₂ - y₁) / (x₂ - x₁).

4. Mối quan hệ giữa Hệ số góc và tính song song, cắt nhau của các đường thẳng

Xét hai đường thẳng có phương trình:

d₁: y = a₁x + b₁
d₂: y = a₂x + b₂

Khi đó:

d₁ song song với d₂ khi và chỉ khi a₁ = a₂ và b₁ ≠ b₂.
d₁ cắt d₂ khi và chỉ khi a₁ ≠ a₂.
d₁ vuông góc với d₂ khi và chỉ khi a₁ * a₂ = -1.

5. Bài tập minh họa

Bài 1: Xác định hệ số góc của đường thẳng y = -2x + 3.

Giải: Hệ số góc của đường thẳng y = -2x + 3 là a = -2.

Bài 2: Cho hai đường thẳng d₁: y = 3x - 1 và d₂: y = 3x + 2. Xác định mối quan hệ giữa hai đường thẳng này.

Giải: Vì a₁ = a₂ = 3 và b₁ ≠ b₂, nên hai đường thẳng d₁ và d₂ song song với nhau.

6. Ứng dụng của Lý thuyết Hệ số góc

Lý thuyết hệ số góc có nhiều ứng dụng trong thực tế, như:

Tính toán độ dốc của đường đi, mái nhà, cầu đường.
Xác định góc nghiêng của các vật thể.
Giải các bài toán liên quan đến hình học phẳng.

Hi vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết Hệ số góc của đường thẳng y = ax + b (a ≠ 0). Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng nó vào giải quyết các bài toán thực tế.