Chào mừng các em học sinh đến với bài học về Lý thuyết Quan hệ giữa xác suất và xác suất thực nghiệm trong chương trình Toán 8. Bài học này sẽ giúp các em hiểu rõ hơn về mối liên hệ giữa lý thuyết xác suất và việc kiểm chứng bằng thực nghiệm.
Chúng ta sẽ cùng nhau khám phá các khái niệm cơ bản, công thức tính toán và các ví dụ minh họa để làm rõ kiến thức này. Hãy cùng bắt đầu!
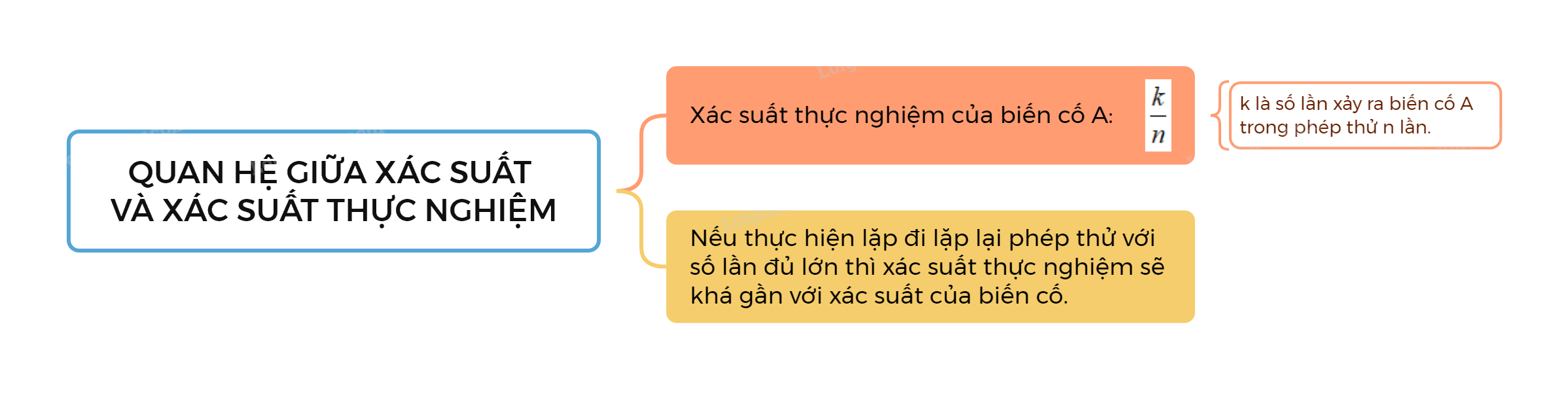
Mối liên hệ giữa xác suất và xác suất thực nghiệm là gì?
1. Xác suất thực nghiệm của biến cố
Định nghĩa:
Nếu thực hiện lặp đi lặp lại một phép thử nào đó n lần và quan sát thấy có k lần xảy ra biến cố A thì tỉ số \(\frac{k}{n}\) được gọi là xác suất thực nghiệm của biến cố A trong n lần thực hiện phép thử.
2. Mối liên hệ giữa xác suất và xác suất thực nghiệm của một biến cố
Nếu thực hiện lặp đi lặp lại một phép thử với số lần đủ lớn thì xác suất thực nghiệm của một biến cố xảy ra trong phép thử sẽ khá gần với xác suất của biến cố đó.
Trong chương trình Toán 8, việc làm quen với khái niệm xác suất là một bước quan trọng trong việc phát triển tư duy logic và khả năng giải quyết vấn đề. Bài học về Quan hệ giữa xác suất và xác suất thực nghiệm giúp học sinh hiểu rõ hơn về cách lý thuyết xác suất được ứng dụng trong thực tế và cách kiểm chứng tính đúng đắn của lý thuyết thông qua các thí nghiệm thực tế.
Xác suất của một sự kiện A, ký hiệu là P(A), là tỷ lệ giữa số kết quả thuận lợi cho A và tổng số kết quả có thể xảy ra trong một thí nghiệm. Công thức tính xác suất là:
P(A) = (Số kết quả thuận lợi cho A) / (Tổng số kết quả có thể xảy ra)
Ví dụ: Gieo một con xúc xắc 6 mặt. Xác suất xuất hiện mặt 5 là 1/6, vì có 1 kết quả thuận lợi (mặt 5) và 6 kết quả có thể xảy ra (các mặt 1, 2, 3, 4, 5, 6).
Xác suất thực nghiệm của một sự kiện A, ký hiệu là Pn(A), là tỷ lệ giữa số lần sự kiện A xảy ra trong n lần thực hiện thí nghiệm và tổng số n lần thực hiện thí nghiệm. Công thức tính xác suất thực nghiệm là:
Pn(A) = (Số lần sự kiện A xảy ra trong n lần thực hiện) / n
Ví dụ: Gieo một đồng xu 20 lần, mặt ngửa xuất hiện 12 lần. Xác suất thực nghiệm của sự kiện “xuất hiện mặt ngửa” là 12/20 = 0.6.
Khi số lần thực hiện thí nghiệm (n) càng lớn, xác suất thực nghiệm Pn(A) sẽ càng gần với xác suất lý thuyết P(A). Đây là một trong những định luật lớn trong lý thuyết xác suất, được gọi là Định luật số lớn.
Điều này có nghĩa là, nếu chúng ta thực hiện một thí nghiệm nhiều lần, kết quả thực tế sẽ càng phản ánh đúng xác suất lý thuyết của sự kiện đó.
Ví dụ 1: Một hộp có 5 quả bóng, trong đó có 2 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất lý thuyết và xác suất thực nghiệm của sự kiện “lấy được quả bóng đỏ” sau 100 lần lấy bóng (có hoàn lại).
Như vậy, xác suất thực nghiệm (0.42) gần với xác suất lý thuyết (0.4).
Ví dụ 2: Tung một đồng xu 500 lần. Ghi lại số lần xuất hiện mặt sấp. Tính xác suất thực nghiệm của sự kiện “xuất hiện mặt sấp”.
Giả sử sau 500 lần tung, mặt sấp xuất hiện 255 lần. Khi đó, xác suất thực nghiệm của sự kiện “xuất hiện mặt sấp” là 255/500 = 0.51.
Xác suất và xác suất thực nghiệm có nhiều ứng dụng trong đời sống và các lĩnh vực khoa học khác nhau, như:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Quan hệ giữa xác suất và xác suất thực nghiệm trong chương trình Toán 8. Chúc các em học tốt!