Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 19, 20 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 được trình bày rõ ràng, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh nắm vững kiến thức Toán 8, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong các kỳ thi.
a) Vẽ đồ thị hai hàm số
Cho hàm số \(y = ax + 2\). Xác định hệ số a, biết đồ thị của hàm số đã cho song song với đường thẳng \(y = - 3x\).
Phương pháp giải:
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại.
Lời giải chi tiết:
Áp dụng điều kiện hai đường thẳng song song, ta suy ra hệ số góc của đường thẳng \(y = ax + 2\) là \(a = - 3\)
a) Vẽ đồ thị hai hàm số \(y = 3x - 2\) và \(y = 3x + 1\) trên cùng một mặt phẳng tọa độ.
b) Giải thích vì sao hai đường thẳng \(y = 3x - 2\) và \(y = 3x + 1\) song song với nhau.
Phương pháp giải:
Vẽ hai đồ thị hàm số trên cùng mặt phẳng tọa độ sau đó giải thích hai đường thẳng song song với nhau bằng cách chứng minh hai góc bằng nhau.
Lời giải chi tiết:
a) Vẽ hệ trục tọa độ \(Oxy\)
Hàm số \(y = 3x - 2\)
Cho \(x = 0 = > y = - 2\)
Cho \(y = 0 = > x = \frac{2}{3}\)
Vậy đồ thị hàm số \(y = 3x - 2\) là đường thẳng đi qua hai điểm \(A\left( {0; - 2} \right),B\left( {\frac{2}{3};0} \right)\)
Hàm số \(y = 3x + 1\)
Cho \(x = 0 = > y = 1\)
Cho \(y = 0 = > x = - \frac{1}{3}\)
Vậy đồ thị hàm số \(y = 3x + 1\) là đường thẳng đi qua hai điểm \(C\left( {0;1} \right),D\left( {\frac{1}{3};0} \right)\)
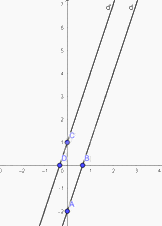
b) Gọi góc tạo bởi đường thẳng \(y = 3x - 2\) và trục \(Ox\) là \({\alpha _1}\)
Góc tạo bởi đường thẳng \(y = 3x + 1\) và trục \(Ox\) là \({\alpha _2}\)
Mà ta thấy cả hai đường thẳng đều có hệ số góc \(a = 3\)
→ Góc \({\alpha _1} = {\alpha _2}\)
Mà hai góc này ở vị trí đồng vị
→ Đường thẳng \(d//d'\)
a) Vẽ đồ thị hai hàm số \(y = 3x - 2\) và \(y = 3x + 1\) trên cùng một mặt phẳng tọa độ.
b) Giải thích vì sao hai đường thẳng \(y = 3x - 2\) và \(y = 3x + 1\) song song với nhau.
Phương pháp giải:
Vẽ hai đồ thị hàm số trên cùng mặt phẳng tọa độ sau đó giải thích hai đường thẳng song song với nhau bằng cách chứng minh hai góc bằng nhau.
Lời giải chi tiết:
a) Vẽ hệ trục tọa độ \(Oxy\)
Hàm số \(y = 3x - 2\)
Cho \(x = 0 = > y = - 2\)
Cho \(y = 0 = > x = \frac{2}{3}\)
Vậy đồ thị hàm số \(y = 3x - 2\) là đường thẳng đi qua hai điểm \(A\left( {0; - 2} \right),B\left( {\frac{2}{3};0} \right)\)
Hàm số \(y = 3x + 1\)
Cho \(x = 0 = > y = 1\)
Cho \(y = 0 = > x = - \frac{1}{3}\)
Vậy đồ thị hàm số \(y = 3x + 1\) là đường thẳng đi qua hai điểm \(C\left( {0;1} \right),D\left( {\frac{1}{3};0} \right)\)
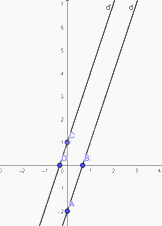
b) Gọi góc tạo bởi đường thẳng \(y = 3x - 2\) và trục \(Ox\) là \({\alpha _1}\)
Góc tạo bởi đường thẳng \(y = 3x + 1\) và trục \(Ox\) là \({\alpha _2}\)
Mà ta thấy cả hai đường thẳng đều có hệ số góc \(a = 3\)
→ Góc \({\alpha _1} = {\alpha _2}\)
Mà hai góc này ở vị trí đồng vị
→ Đường thẳng \(d//d'\)
Cho hàm số \(y = ax + 2\). Xác định hệ số a, biết đồ thị của hàm số đã cho song song với đường thẳng \(y = - 3x\).
Phương pháp giải:
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại.
Lời giải chi tiết:
Áp dụng điều kiện hai đường thẳng song song, ta suy ra hệ số góc của đường thẳng \(y = ax + 2\) là \(a = - 3\)
Mục 2 của chương trình Toán 8, trang 19 và 20 sách giáo khoa, thường tập trung vào các kiến thức cơ bản về hình học, cụ thể là các định lý và tính chất liên quan đến tứ giác. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Để giải các bài tập trong mục này một cách hiệu quả, các em cần:
Giải:
Áp dụng tính chất tổng các góc trong một tứ giác, ta có:
Góc D = 360 độ - (góc A + góc B + góc C)
Góc D = 360 độ - (80 độ + 100 độ + 110 độ)
Góc D = 360 độ - 290 độ
Góc D = 70 độ
Giải:
Vì AB // CD nên:
Góc A + góc D = 180 độ (hai góc kề trong)
Góc B + góc C = 180 độ (hai góc kề trong)
Ta có: Góc A = 60 độ, góc D = 120 độ (đã cho)
Góc B = 180 độ - góc A = 180 độ - 60 độ = 120 độ
Góc C = 180 độ - góc D = 180 độ - 120 độ = 60 độ
Các bài tập trong mục này thường xoay quanh việc:
Để học tốt môn Toán 8, đặc biệt là phần hình học, các em nên:
Hy vọng với bài giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 19, 20 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao!