Chào mừng bạn đến với bài học về lý thuyết cộng, trừ các phân thức đại số, một phần quan trọng trong chương trình Toán 8. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để giải quyết các bài toán liên quan đến phân thức đại số một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng dễ hiểu, bài tập thực hành đa dạng và phương pháp học tập tối ưu nhất.
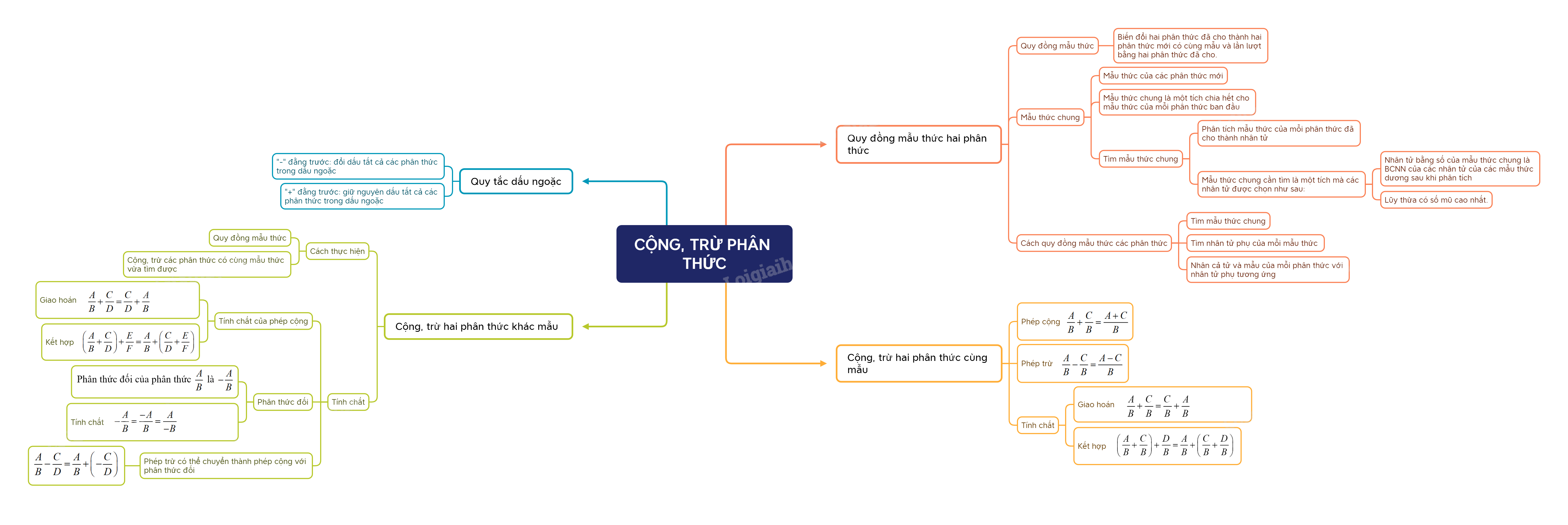
Quy đồng mẫu thức là gì?
1. Quy đồng mẫu thức
- Quy đồng mẫu thức các phân thức là biến đổi chúng thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức ban đầu.
- Mẫu thức của những phân thức mới đó gọi là mẫu thức chung.
Lưu ý:
- Mẫu thức chung thường được chọn là một tích chia hết cho mẫu thức của mỗi phân thức ban đầu.
- Các bước tìm mẫu thức chung:
+ Phân tích mẫu thức của mỗi phân thức đã cho thành nhân tử
+ Mẫu thức chung cần tìm là một tích mà các nhân tử được chọn như sau:
* Nhân tử bằng số của mẫu thức chung là tích các nhân tử bằng số của các mẫu dương ở Bước 1 (nếu các nhân tử bằng số của các mẫu thức là các số nguyên dương thì nhân tử bằng số của mẫu thức chung là BCNN của chúng);
* Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa có số mũ cao nhất.
- Cácbước quy đồng mẫu thức các phân thức:
+ Tìm mẫu thức chung
+ Tìm nhân tử phụ của mỗi mẫu thức (là đa thức thỏa mãn tích của nó và mẫu thức bằng mẫu thức chung)
+ Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng
2. Cộng, trừ hai phân thức cùng mẫu thức
Quy tắc cộng hai phân thức có cùng mẫu thức
Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức.
\(\frac{A}{B} + \frac{C}{B} = \frac{{A + C}}{B}; \frac{A}{B} - \frac{C}{B} = \frac{{A - C}}{B}\)
Chú ý: Phép cộng phân thức có các tính chất giao hoán, kết hợp tương tự như đối với phân số.
Ví dụ:
\(\begin{array}{l}\frac{{x + y}}{{xy}} + \frac{{x - y}}{{xy}} = \frac{{x + y + x - y}}{{xy}} = \frac{{2x}}{{xy}} = \frac{2}{y}\\\frac{x}{{x + 3}} + \frac{{2 - x}}{{x + 3}} = \frac{{x + 2 - x}}{{x + 3}} = \frac{2}{{x + 3}}\end{array}\)
3. Cộng hai phân thức khác mẫu thức
Muốn cộng hai phân thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
Chú ý: Phép cộng các phân thức cũng có các tính chất giao hoán, kết hợp:
\(\frac{A}{B} + \frac{C}{D} = \frac{C}{D} + \frac{A}{B}; \left( {\frac{A}{B} + \frac{C}{D}} \right) + \frac{E}{F} = \frac{A}{B} + \left( {\frac{C}{D} + \frac{E}{F}} \right)\) , trong đó \(\frac{A}{B};\frac{C}{D};\frac{E}{F}\) là các phân thức bất kì.
4. Trừ hai phân thức khác mẫu (Quy tắc trừ hai phân thức khác mẫu thức)
Muốn trừ phân thức \(\frac{A}{B}\) cho phân thức \(\frac{C}{D}\), ta cộng \(\frac{A}{B}\) với phân thức đối của \(\frac{C}{D}\)
\(\frac{A}{B} - \frac{C}{D} = \frac{A}{B} + \left( { - \frac{C}{D}} \right)\)
Ví dụ:
\(\frac{{x + 1}}{{x - 2}} - \frac{{x - 3}}{{x - 2}} = \frac{{x + 1 - x + 3}}{{x - 2}} = \frac{4}{{x - 2}}\)
\(\frac{3}{{2x - 4y}} - \frac{2}{{3x - 6y}} = \frac{3}{{2(x - 2y)}} - \frac{2}{{3(x - 2y)}} = \frac{{3.3}}{{6(x - 2y)}} - \frac{{2.2}}{{6(x - 2y)}} = \frac{{9 - 4}}{{6(x - 2y)}} = \frac{5}{{6(x - 2y)}}\)
5. Quy tắc dấu ngoặc
- Khi bỏ dấu ngoặc mà có dấu “-“ đằng trước thì ta phải đổi dấu tất cả các phân thức trong dấu ngoặc
- Khi bỏ dấu ngoặc mà có dấu “+“ đằng trước thì ta giữ nguyên dấu tất cả các phân thức trong dấu ngoặc
Ví dụ:
\(\begin{array}{l}\left( { - \frac{x}{{{x^2} - {y^2}}} + \frac{{2y + x}}{{x + y}}} \right) - \left( {\frac{y}{{x + y}} - \frac{x}{{{x^2} - {y^2}}}} \right)\\ = - \frac{x}{{{x^2} - {y^2}}} + \frac{{2y + x}}{{x + y}} - \frac{y}{{x + y}} + \frac{x}{{{x^2} - {y^2}}}\\ = \left( { - \frac{x}{{{x^2} - {y^2}}} + \frac{x}{{{x^2} - {y^2}}}} \right) + \left( {\frac{{2y + x}}{{x + y}} - \frac{y}{{x + y}}} \right)\\ = 0 + \frac{{y + x}}{{x + y}} = 1\end{array}\)
Phân thức đại số là một biểu thức toán học quan trọng trong chương trình Toán 8, và việc nắm vững các quy tắc cộng, trừ phân thức là nền tảng để giải quyết các bài toán phức tạp hơn. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và các bài tập thực hành để giúp bạn hiểu rõ và áp dụng thành thạo kiến thức này.
Một phân thức đại số là một biểu thức có dạng P/Q, trong đó P và Q là các đa thức, và Q khác 0. P được gọi là tử số, Q được gọi là mẫu số.
Một phân thức đại số chỉ xác định khi mẫu số khác 0. Điều này có nghĩa là chúng ta cần tìm các giá trị của biến sao cho mẫu số không bằng 0.
Để cộng hoặc trừ các phân thức đại số, chúng ta cần thực hiện các bước sau:
Ví dụ 1: Cộng hai phân thức sau:
1/2x + 1/3y
Giải:
Ví dụ 2: Trừ hai phân thức sau:
x/x+1 - 1/x
Giải:
Hãy thực hiện các bài tập sau để củng cố kiến thức:
Khi cộng hoặc trừ các phân thức đại số, hãy luôn nhớ:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết cộng, trừ các phân thức đại số. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Chúc bạn học tập tốt!