Chào mừng các em học sinh đến với bài giải chi tiết bài 7.10 trang 95 SGK Toán 8. Bài tập này thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Tìm hiểu số bác sĩ trực thuộc Sở Y tế các tỉnh vùng Tây Nguyên, Dũng và Đức thu được bảng số liệu sau:
Đề bài
Tìm hiểu số bác sĩ trực thuộc Sở Y tế các tỉnh vùng Tây Nguyên, Dũng và Đức thu được bảng số liệu sau:
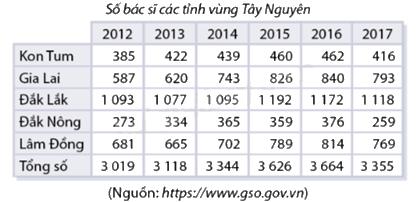
Dũng tính tỉ lệ bác sĩ của các tỉnh so với toàn vùng năm \(2012.\) Sau khi làm tròn số, Dũng dùng biểu đồ hình quạt tròn để biểu diễn dữ liệu. Còn Đức biểu diễn dữ liệu năm 2012 bằng một biểu đồ cột.
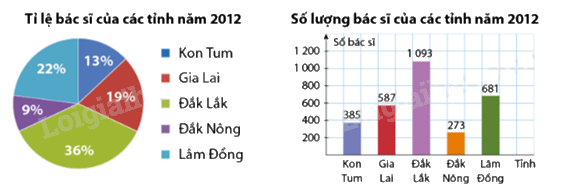
a) Nếu muốn có một hình ảnh trực quan để so sánh tỉ lệ bác sĩ giữa các tỉnh với toàn vùng năm \(2012\) thì lựa chọn của ai tốt hơn? Vì sao?
b) Trong hai biểu đồ đó, có một biểu đồ sai. Đó là biểu đồ nào? Giải thích ý kiến của em.
c) Vẽ biểu đồ có thể dùng để phân tích xu hướng thay đổi số bác sĩ toàn vùng Tây Nguyên giai đoạn \(2012 - 2017.\)
Phương pháp giải - Xem chi tiết
Biểu đồ quạt trong thể hiện tốt nhất tỉ lệ giữa các nhóm đối tượng với toàn thể tập hợp đối tượng điều tra.
Biểu đồ cột giúp ta dễ dàng so sánh các dãy số liệu chỉ liên quan đến một đặc tính.
Lời giải chi tiết
a) Nếu muốn có một hình ảnh trực qua để so sánh tỉ lệ bác sĩ giữa các tỉnh với toàn vùng năm 2012 thì lựa chọn của Dũng tốt hơn. Bởi vì biểu đồ quạt tròn thể hiện tốt nhất tỉ lệ giữa các nhóm đối tượng với toàn thể tập hợp đối tượng điều tra.
b) Biểu đồ của Đức là sau. Bởi vì biểu đồ cột là biểu đồ chỉ liên quan đến một đặc tính của đối tượng điều tra. Khi Đức vẽ biểu đồ cột như trên thì các cột không phải cùng một đặc tính và không biểu hiện rõ tỉ lệ của năm 2012 so với toàn vùng.
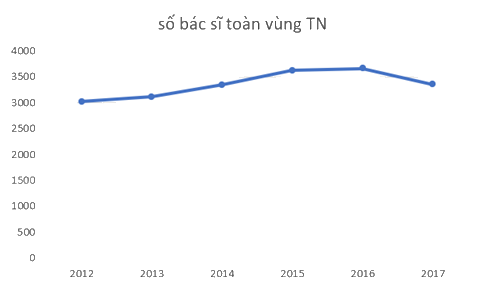
c) Để phân tích xu hướng thay đổi số bác sĩ toàn vùng Tây Nguyên giai đoạn 2012-2017, ta có thể vẽ biểu đồ đoạn thẳng.
Biểu đồ thể hiện xu hướng thay đổi số bác sĩ toàn vùng Tây Nguyên giai đoạn 2012-2017
Bài 7.10 trang 95 SGK Toán 8 yêu cầu học sinh vận dụng kiến thức về hình thang cân để giải quyết các bài toán liên quan đến tính chất đường trung bình, đường cao và các yếu tố khác của hình thang cân. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và định lý sau:
Để giải bài 7.10 trang 95 SGK Toán 8, chúng ta cần phân tích kỹ đề bài, xác định các yếu tố đã cho và yêu cầu của bài toán. Sau đó, áp dụng các kiến thức và công thức đã học để tìm ra lời giải chính xác.
Ví dụ minh họa: (Giả sử đề bài yêu cầu tính độ dài đường cao của hình thang cân khi biết độ dài hai đáy và cạnh bên)
Ngoài bài 7.10, còn rất nhiều bài tập tương tự liên quan đến hình thang cân. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, các em nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. Việc luyện tập thường xuyên sẽ giúp các em hiểu sâu hơn về các khái niệm và định lý, đồng thời rèn luyện khả năng giải quyết các bài toán một cách nhanh chóng và chính xác.
Giaitoan.edu.vn tự hào là một trong những website học toán online uy tín và chất lượng hàng đầu tại Việt Nam. Chúng tôi cung cấp đầy đủ các bài giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong SGK Toán 8, cũng như các bài tập nâng cao và luyện thi. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều kiến thức và tài liệu hữu ích khác nhé!
| Khái niệm | Định nghĩa |
|---|---|
| Hình thang cân | Hình thang có hai cạnh bên bằng nhau |
| Đường trung bình | Đoạn thẳng nối trung điểm hai cạnh bên, bằng nửa tổng hai đáy |