Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi xin giới thiệu bộ giải chi tiết các bài tập trong mục 2, trang 19, 20, 21, 22, 23, 24 sách giáo khoa Toán 8.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của từng bài toán, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Cho
Tính:
a) \({\left( {a + 4} \right)^2}\);
b) \({\left( {2u + 5v} \right)^2}\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Để thực hiện phép tính.
Lời giải chi tiết:
a) \({\left( {a + 4} \right)^2} = {a^2} + 2.a.4 + {4^2} = {a^2} + 8a + 16\)
b) \({\left( {2u + 5v} \right)^2} = {\left( {2u} \right)^2} + 2.2u.5v + {\left( {5v} \right)^2} = 4{u^2} + 20uv + 25{v^2}\)
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a + b} \right)\left( {a + b} \right)\)
2. Hãy cho biết: \({\left( {a + b} \right)^2} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. Ta có \(\left( {a + b} \right)\left( {a + b} \right) = aa + ab + ab + bb = {a^2} + 2ab + {b^2}\)
2. Có \({\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {a + b} \right) = {a^2} + 2ab + {b^2}\)
Viết các biểu thức sau dưới dạng bình phương của một tổng:
a) \(16{a^2} + 8a + 1\);
b) \({x^2} + 25{y^2} + 10xy\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Để phân tích biểu thức và viết lại dưới dạng bình phương của một tổng.
Lời giải chi tiết:
a) Ta có \(16{a^2} + 8a + 1 = {\left( {4a} \right)^2} + 2.4a.1 + {1^2} = {\left( {4a + 1} \right)^2}\)
b) Ta có\({x^2} + 25{y^2} + 10xy = {x^2} + 2.x.5y + {\left( {5y} \right)^2} = {\left( {x + 5y} \right)^2}\).
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a - b} \right)\left( {a - b} \right)\).
2. Hãy cho biết \({\left( {a - b} \right)^2}\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1.Ta có \(\left( {a - b} \right)\left( {a - b} \right) = a\left( {a - b} \right) - b\left( {a - b} \right) = {a^2} - ab - ab + {b^2} = {a^2} - 2ab + {b^2}\)
2. Có \({\left( {a - b} \right)^2} = \left( {a - b} \right)\left( {a - b} \right) = {a^2} - 2ab + {b^2}\)
Tính:
a) \({\left( {3a - 1} \right)^2}\)
b) \({\left( {4u - 5v} \right)^2}\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Để thực hiện phép tính
Lời giải chi tiết:
a) \({\left( {3a - 1} \right)^2} = {\left( {3a} \right)^2} - 2.3a.1 + {1^2} = 9{a^2} - 6a + 1\)
b) \({\left( {4u - 5v} \right)^2} = {\left( {4u} \right)^2} - 2.4u.5v + {\left( {5v} \right)^2} = 16{u^2} - 40uv + 25{v^2}\)
Viết các biểu thức sau dưới dạng bình phương của một hiệu:
a) \({a^2} - 12a + 36\);
b) \(25{x^2} + 64{y^2} - 80xy\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Để viết lại biểu thức dưới dạng bình phương của một hiệu.
Lời giải chi tiết:
a) Ta có \({a^2} - 12a + 36 = {a^2} - 2.a.6 + {6^2} = {\left( {a - 6} \right)^2}\);
b) Ta có \(25{x^2} + 64{y^2} - 80xy = {\left( {5x} \right)^2} - 2.5x.8y + {\left( {8y} \right)^2} = {\left( {5x - 8y} \right)^2}\).
Cho \(a\) và \(b\) là hai số thực bất kì.
1. \(\left( {a + b} \right)\left( {a - b} \right)\).
2. Hãy cho biết: \({a^2} - {b^2} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. Ta có \(\left( {a + b} \right)\left( {a - b} \right) = a\left( {a - b} \right) + b\left( {a - b} \right) = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)
2. Vậy \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
Tính:
a) \(\left( {2a + 1} \right)\left( {2a - 1} \right)\)
b)\(\left( {2x + 5y} \right)\left( {2x - 5y} \right)\)
Phương pháp giải:
Sử dụng hằng đẳng thức \(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}\) để thực hiện phép tính.
Lời giải chi tiết:
a) \(\left( {2a + 1} \right)\left( {2a - 1} \right) = {\left( {2a} \right)^2} - {1^2} = 4{a^2} - 1\)
b) \(\left( {2x + 5y} \right)\left( {2x - 5y} \right) = {\left( {2x} \right)^2} - {\left( {5y} \right)^2} = 4{x^2} - 25{y^2}\)
Tính nhanh:
a) \(49.51\)
b) \({32^2} - 128 + 4\)
Phương pháp giải:
Sử dụng hằng đẳng thức \(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}\) để thực hiện phép tính một cách nhanh nhất
Lời giải chi tiết:
a) Ta thấy \(49.51 = \left( {50 - 1} \right)\left( {50 + 1} \right) = {50^2} - {1^2} = 2500 - 1 = 2499\)
b) \({32^2} - 128 + 4 = {32^2} - 144 = {32^2} - {12^2} = \left( {32 - 12} \right)\left( {32 + 12} \right) = 20.44 = 880\)
Cho \(a\) và \(b\)là hai số thực bất kì:
Phương pháp giải:
1. Sử dụng hằng đẳng thức bình phương của một tổng kết hợp với nhân đa thức với đa thức để thực hiện phép tính.
2. Dựa vào kết quả của ý 1.
Lời giải chi tiết:
1. \(\left( {a + b} \right){\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {{a^2} + 2ab + {b^2}} \right) = {a^3} + {a^2}b + 2{a^2}b + 2a{b^2} + a{b^2} + {b^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)
2. Có \({\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)
Tính:
a)\({\left( {2a + 3} \right)^3}\)
b)\({\left( {u + 4v} \right)^3}\)
Phương pháp giải:
Sử dụng hằng đẳng thức \({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) thực hiện phép tính.
Lời giải chi tiết:
a) \({\left( {2a + 3} \right)^3} = {\left( {2a} \right)^3} + 3.{\left( {2a} \right)^2}.3 + 3.2a{.3^2} + {3^3} = 8{a^3} + 36{a^2} + 54a + 27\)
b) \({\left( {u + 4v} \right)^3} = {u^3} + 3.{u^2}.4v + 3.u.{\left( {4v} \right)^2} + {\left( {4v} \right)^3} = {u^3} + 12{u^2}v + 48u{v^2} + 64{v^3}\)
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \({\left[ {a + \left( { - b} \right)} \right]^3}\).
2. Hãy cho biết: \({\left( {a - b} \right)^3} = ?\).
Phương pháp giải:
1. Ta nhân đa thức với đa thức kết hợp với sử dụng hằng đẳng thức bình phương của một hiệu: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1.Ta có:
\(\begin{array}{l}{\left[ {a + \left( { - b} \right)} \right]^3} = {\left( {a - b} \right)^2}\left( {a - b} \right) = \left( {{a^2} - 2ab + {b^2}} \right)\left( {a - b} \right)\\ = {a^3} - 2{a^2}b + a{b^2} + 2a{b^2} - {a^2}b - {b^3}\\ = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\end{array}\)
2. \({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}.\)
Tính:
a) \({\left( {a - 3} \right)^3};\)
b) \({\left( {3u - 4v} \right)^3}.\)
Phương pháp giải:
Sử dụng hằng đẳng thức \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) thực hiện phép tính.
Lời giải chi tiết:
a)
\(\begin{array}{l}{\left( {a - 3} \right)^3} = {a^3} - 3.{a^2}.3 + 3.a{.3^2} - {3^3}\\ = {a^3} - 9{a^2} + 27a - 27\end{array}\)
b)
\(\begin{array}{l}{\left( {3u - 4v} \right)^3} = {\left( {3u} \right)^3} - 3.{\left( {3u} \right)^2}.4v + 3.3u.{\left( {4v} \right)^2} - {\left( {4v} \right)^2}\\ = 27{u^3} - 108{u^2}v + 144u{v^2} - 64{v^3}\end{array}\)
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right).\)
2. Hãy cho biết \({a^3} + {b^3} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. Ta có:
\(\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right) = {a^3} - {a^2}b + a{b^2} + {a^2}b - a{b^2} + {b^3} = {a^3} + {b^3}.\)
2. \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\)
a) Viết \(8{a^3} + 27\) dưới dạng tích.
b) Viết \(\left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right)\) dưới dạng tổng.
Phương pháp giải:
Sử dụng hằng đẳng thức \({A^3} + {B^3} = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)\) thực hiện phép tính.
Lời giải chi tiết:
a) \(8{a^3} + 27 = {\left( {2a} \right)^3} + {3^3} = \left( {2a + 3} \right)\left( {4{a^2} - 6a + 9} \right)\)
b) \(\left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right) = {x^3} + 27\)
Cho \(a\) và \(b\) là hai số thực bất kì.
a) Thực hiện phép tính \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)
b) \({a^3} - {b^3} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) = {a^3} + {a^2}b + a{b^2} - {a^2}b - a{b^2} - {b^3} = {a^3} - {b^3}.\)
2. \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)
a) Tính \(\left( {a - 4} \right)\left( {{a^2} + 4a + 16} \right).\)
b) Viết \(64{x^3} - 27{y^3}\) dưới dạng tích.
Phương pháp giải:
Sử dụng hằng đẳng thức \({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)\) thực hiện phép tính.
Lời giải chi tiết:
a) \(\left( {a - 4} \right)\left( {{a^2} + 4a + 16} \right) = {a^3} - {4^3} = {a^3} - 64\)
b) \(64{x^3} - 27{y^3} = {\left( {4x} \right)^3} - {\left( {3y} \right)^3} = \left( {4x - 3y} \right)\left( {16{x^2} - 12xy + 9{y^2}} \right)\)
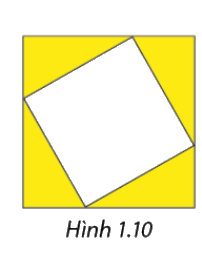
Một người dùng các thanh kim loại để thiết kế một khung ảnh gồm hai hình vuông lồng vào nhau như Hình 1.10, trong đó ảnh được gắn vào hình vuông nhỏ. Biết rằng tổng chiều dài của các thanh kim loại để làm khung là \(168\,\,cm\) và diện tích phần không gắn ảnh( phần tô màu) là \(252\,\,c{m^2}\). Tính diện tích của phần được gắn ảnh.
Phương pháp giải:
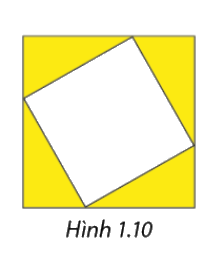
Gọi độ dài hai cạnh hình vuông lần lượt là\(a\) và \(b\)như hình vẽ
Viết biểu thức biểu diễn tổng chiều dài của các thanh kim loại.
Viết biểu thức biểu diễn diện tích phần không gắn ảnh.
Áp dụng các kiến thức đã học để tính diện tích phần tô màu.
Lời giải chi tiết:
Gọi độ dài hai cạnh hình vuông lần lượt là \(a\) và \(b\)như hình vẽ \(\left( {cm,a > b > 0} \right)\)
Theo đề bài tổng độ dài của các thanh kim loại là \(168cm\)nên ta có: \(4a + 4b = 168 \Rightarrow a + b = 42\)(1)
Diện tích phần không gắn ảnh là hiệu diện tích của hình vuông lớn và hình vuông nhỏ và bằng \(252c{m^2}\)nên ta có: \({a^2} - {b^2} = 252 \Rightarrow \left( {a + b} \right)\left( {a - b} \right) = 252 \Rightarrow 42.\left( {a - b} \right) = 252 \Rightarrow a - b = 6\)
\( \Rightarrow a = 6 + b\)Thay vào (1) ta có: \(6 + b + b = 42 \Rightarrow 2b = 36 \Rightarrow b = 18 \Rightarrow a = 24\)
Diện tích phần không gắn ảnh là: \(4.\frac{1}{2}ab = 2ab\)\(c{m^2}\)
Có \(2ab = 252\) nên \(ab = 126 \Rightarrow a = \frac{{126}}{b}\)
Thay \(a = \frac{{126}}{b}\)vào (1) ta được \(\begin{array}{l}4.\frac{{126}}{b} + 4b + {\left( {\frac{{126}}{b}} \right)^2} - {b^2} = 168\\ \Rightarrow 504 + 4{b^2} + {126^2} - {b^3}\end{array}\)
Diện tích của phần được gắn ảnh là:
Trong Hình 1.9, diện tích của hình vuông là \(9m - 42m + 49\), với \(m > 3\).
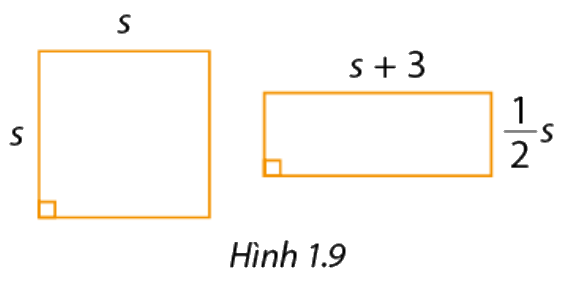
a) Tìm độ dài cạnh hình vuông theo \(m\). Từ đó biểu diễn \(s\)theo \(m\).
b) Tính diện tích hình chữ nhật trong hình 1.9 theo \(m\).
Phương pháp giải:
a) Viết lại biểu thức biểu diễn diện tích hình vuông dưới dạng bình phương của một hiệu. Từ đó suy ra độ dài cạnh của hình vuông đó
b) Viết biểu thức tính diện tích hình chữ nhật theo công thức tính diện tích hình chữ nhật.
Lời giải chi tiết:
a) Với \(m > 3\)ta có
\(9{m^2} - 42m + 49 = {\left( {3m} \right)^2} - 2.3m.7 + {7^2} = {\left( {3m - 7} \right)^2}\)
Vậy độ dài cạnh hình vuông là \(3m - 7\)
Vậy \(s = 3m - 7\)
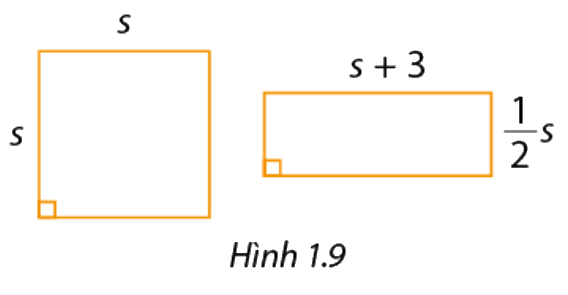
b) Diện tích hình chữ nhật trong hình 1.9 là:
\(\left( {s + 3} \right).\frac{1}{2}s = \left( {3m - 7 + 3} \right).\frac{1}{2}\left( {3m - 7} \right) = \frac{1}{2}\left( {3m - 4} \right)\left( {3m - 7} \right)\)
\( = \frac{1}{2}\left( {9{m^2} - 21m - 12m + 28} \right) = \frac{1}{2}\left( {9{m^2} - 33m + 28} \right) = \frac{9}{2}{m^2} - \frac{{33}}{2}m + 14\)
Vậy diện tích hình chữ nhật trong hình 1.9 là \(\frac{9}{2}{m^2} - \frac{{33}}{2}m + 14\).
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a + b} \right)\left( {a + b} \right)\)
2. Hãy cho biết: \({\left( {a + b} \right)^2} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. Ta có \(\left( {a + b} \right)\left( {a + b} \right) = aa + ab + ab + bb = {a^2} + 2ab + {b^2}\)
2. Có \({\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {a + b} \right) = {a^2} + 2ab + {b^2}\)
Tính:
a) \({\left( {a + 4} \right)^2}\);
b) \({\left( {2u + 5v} \right)^2}\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Để thực hiện phép tính.
Lời giải chi tiết:
a) \({\left( {a + 4} \right)^2} = {a^2} + 2.a.4 + {4^2} = {a^2} + 8a + 16\)
b) \({\left( {2u + 5v} \right)^2} = {\left( {2u} \right)^2} + 2.2u.5v + {\left( {5v} \right)^2} = 4{u^2} + 20uv + 25{v^2}\)
Viết các biểu thức sau dưới dạng bình phương của một tổng:
a) \(16{a^2} + 8a + 1\);
b) \({x^2} + 25{y^2} + 10xy\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một tổng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Để phân tích biểu thức và viết lại dưới dạng bình phương của một tổng.
Lời giải chi tiết:
a) Ta có \(16{a^2} + 8a + 1 = {\left( {4a} \right)^2} + 2.4a.1 + {1^2} = {\left( {4a + 1} \right)^2}\)
b) Ta có\({x^2} + 25{y^2} + 10xy = {x^2} + 2.x.5y + {\left( {5y} \right)^2} = {\left( {x + 5y} \right)^2}\).
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a - b} \right)\left( {a - b} \right)\).
2. Hãy cho biết \({\left( {a - b} \right)^2}\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1.Ta có \(\left( {a - b} \right)\left( {a - b} \right) = a\left( {a - b} \right) - b\left( {a - b} \right) = {a^2} - ab - ab + {b^2} = {a^2} - 2ab + {b^2}\)
2. Có \({\left( {a - b} \right)^2} = \left( {a - b} \right)\left( {a - b} \right) = {a^2} - 2ab + {b^2}\)
Tính:
a) \({\left( {3a - 1} \right)^2}\)
b) \({\left( {4u - 5v} \right)^2}\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Để thực hiện phép tính
Lời giải chi tiết:
a) \({\left( {3a - 1} \right)^2} = {\left( {3a} \right)^2} - 2.3a.1 + {1^2} = 9{a^2} - 6a + 1\)
b) \({\left( {4u - 5v} \right)^2} = {\left( {4u} \right)^2} - 2.4u.5v + {\left( {5v} \right)^2} = 16{u^2} - 40uv + 25{v^2}\)
Viết các biểu thức sau dưới dạng bình phương của một hiệu:
a) \({a^2} - 12a + 36\);
b) \(25{x^2} + 64{y^2} - 80xy\)
Phương pháp giải:
Dựa vào hằng đẳng thức bình phương của một hiệu: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Để viết lại biểu thức dưới dạng bình phương của một hiệu.
Lời giải chi tiết:
a) Ta có \({a^2} - 12a + 36 = {a^2} - 2.a.6 + {6^2} = {\left( {a - 6} \right)^2}\);
b) Ta có \(25{x^2} + 64{y^2} - 80xy = {\left( {5x} \right)^2} - 2.5x.8y + {\left( {8y} \right)^2} = {\left( {5x - 8y} \right)^2}\).
Trong Hình 1.9, diện tích của hình vuông là \(9m - 42m + 49\), với \(m > 3\).
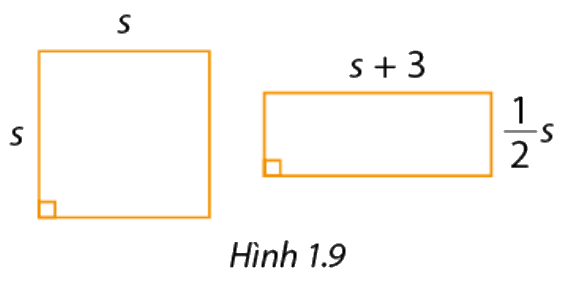
a) Tìm độ dài cạnh hình vuông theo \(m\). Từ đó biểu diễn \(s\)theo \(m\).
b) Tính diện tích hình chữ nhật trong hình 1.9 theo \(m\).
Phương pháp giải:
a) Viết lại biểu thức biểu diễn diện tích hình vuông dưới dạng bình phương của một hiệu. Từ đó suy ra độ dài cạnh của hình vuông đó
b) Viết biểu thức tính diện tích hình chữ nhật theo công thức tính diện tích hình chữ nhật.
Lời giải chi tiết:
a) Với \(m > 3\)ta có
\(9{m^2} - 42m + 49 = {\left( {3m} \right)^2} - 2.3m.7 + {7^2} = {\left( {3m - 7} \right)^2}\)
Vậy độ dài cạnh hình vuông là \(3m - 7\)
Vậy \(s = 3m - 7\)
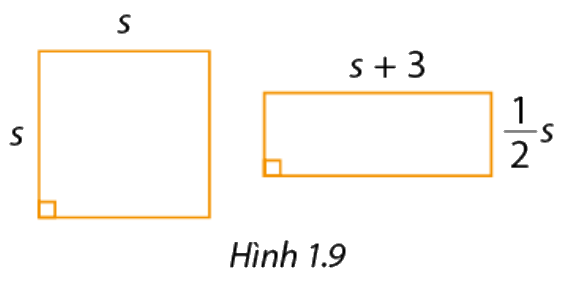
b) Diện tích hình chữ nhật trong hình 1.9 là:
\(\left( {s + 3} \right).\frac{1}{2}s = \left( {3m - 7 + 3} \right).\frac{1}{2}\left( {3m - 7} \right) = \frac{1}{2}\left( {3m - 4} \right)\left( {3m - 7} \right)\)
\( = \frac{1}{2}\left( {9{m^2} - 21m - 12m + 28} \right) = \frac{1}{2}\left( {9{m^2} - 33m + 28} \right) = \frac{9}{2}{m^2} - \frac{{33}}{2}m + 14\)
Vậy diện tích hình chữ nhật trong hình 1.9 là \(\frac{9}{2}{m^2} - \frac{{33}}{2}m + 14\).
Cho \(a\) và \(b\) là hai số thực bất kì.
1. \(\left( {a + b} \right)\left( {a - b} \right)\).
2. Hãy cho biết: \({a^2} - {b^2} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. Ta có \(\left( {a + b} \right)\left( {a - b} \right) = a\left( {a - b} \right) + b\left( {a - b} \right) = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)
2. Vậy \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
Tính:
a) \(\left( {2a + 1} \right)\left( {2a - 1} \right)\)
b)\(\left( {2x + 5y} \right)\left( {2x - 5y} \right)\)
Phương pháp giải:
Sử dụng hằng đẳng thức \(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}\) để thực hiện phép tính.
Lời giải chi tiết:
a) \(\left( {2a + 1} \right)\left( {2a - 1} \right) = {\left( {2a} \right)^2} - {1^2} = 4{a^2} - 1\)
b) \(\left( {2x + 5y} \right)\left( {2x - 5y} \right) = {\left( {2x} \right)^2} - {\left( {5y} \right)^2} = 4{x^2} - 25{y^2}\)
Tính nhanh:
a) \(49.51\)
b) \({32^2} - 128 + 4\)
Phương pháp giải:
Sử dụng hằng đẳng thức \(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}\) để thực hiện phép tính một cách nhanh nhất
Lời giải chi tiết:
a) Ta thấy \(49.51 = \left( {50 - 1} \right)\left( {50 + 1} \right) = {50^2} - {1^2} = 2500 - 1 = 2499\)
b) \({32^2} - 128 + 4 = {32^2} - 144 = {32^2} - {12^2} = \left( {32 - 12} \right)\left( {32 + 12} \right) = 20.44 = 880\)
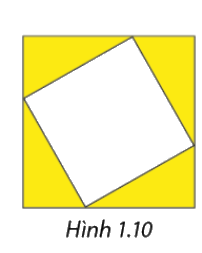
Một người dùng các thanh kim loại để thiết kế một khung ảnh gồm hai hình vuông lồng vào nhau như Hình 1.10, trong đó ảnh được gắn vào hình vuông nhỏ. Biết rằng tổng chiều dài của các thanh kim loại để làm khung là \(168\,\,cm\) và diện tích phần không gắn ảnh( phần tô màu) là \(252\,\,c{m^2}\). Tính diện tích của phần được gắn ảnh.
Phương pháp giải:
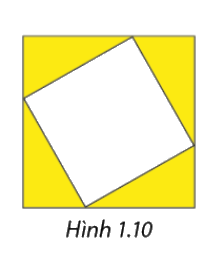
Gọi độ dài hai cạnh hình vuông lần lượt là\(a\) và \(b\)như hình vẽ
Viết biểu thức biểu diễn tổng chiều dài của các thanh kim loại.
Viết biểu thức biểu diễn diện tích phần không gắn ảnh.
Áp dụng các kiến thức đã học để tính diện tích phần tô màu.
Lời giải chi tiết:
Gọi độ dài hai cạnh hình vuông lần lượt là \(a\) và \(b\)như hình vẽ \(\left( {cm,a > b > 0} \right)\)
Theo đề bài tổng độ dài của các thanh kim loại là \(168cm\)nên ta có: \(4a + 4b = 168 \Rightarrow a + b = 42\)(1)
Diện tích phần không gắn ảnh là hiệu diện tích của hình vuông lớn và hình vuông nhỏ và bằng \(252c{m^2}\)nên ta có: \({a^2} - {b^2} = 252 \Rightarrow \left( {a + b} \right)\left( {a - b} \right) = 252 \Rightarrow 42.\left( {a - b} \right) = 252 \Rightarrow a - b = 6\)
\( \Rightarrow a = 6 + b\)Thay vào (1) ta có: \(6 + b + b = 42 \Rightarrow 2b = 36 \Rightarrow b = 18 \Rightarrow a = 24\)
Diện tích phần không gắn ảnh là: \(4.\frac{1}{2}ab = 2ab\)\(c{m^2}\)
Có \(2ab = 252\) nên \(ab = 126 \Rightarrow a = \frac{{126}}{b}\)
Thay \(a = \frac{{126}}{b}\)vào (1) ta được \(\begin{array}{l}4.\frac{{126}}{b} + 4b + {\left( {\frac{{126}}{b}} \right)^2} - {b^2} = 168\\ \Rightarrow 504 + 4{b^2} + {126^2} - {b^3}\end{array}\)
Diện tích của phần được gắn ảnh là:
Cho \(a\) và \(b\)là hai số thực bất kì:
Phương pháp giải:
1. Sử dụng hằng đẳng thức bình phương của một tổng kết hợp với nhân đa thức với đa thức để thực hiện phép tính.
2. Dựa vào kết quả của ý 1.
Lời giải chi tiết:
1. \(\left( {a + b} \right){\left( {a + b} \right)^2} = \left( {a + b} \right)\left( {{a^2} + 2ab + {b^2}} \right) = {a^3} + {a^2}b + 2{a^2}b + 2a{b^2} + a{b^2} + {b^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)
2. Có \({\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)
Tính:
a)\({\left( {2a + 3} \right)^3}\)
b)\({\left( {u + 4v} \right)^3}\)
Phương pháp giải:
Sử dụng hằng đẳng thức \({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) thực hiện phép tính.
Lời giải chi tiết:
a) \({\left( {2a + 3} \right)^3} = {\left( {2a} \right)^3} + 3.{\left( {2a} \right)^2}.3 + 3.2a{.3^2} + {3^3} = 8{a^3} + 36{a^2} + 54a + 27\)
b) \({\left( {u + 4v} \right)^3} = {u^3} + 3.{u^2}.4v + 3.u.{\left( {4v} \right)^2} + {\left( {4v} \right)^3} = {u^3} + 12{u^2}v + 48u{v^2} + 64{v^3}\)
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \({\left[ {a + \left( { - b} \right)} \right]^3}\).
2. Hãy cho biết: \({\left( {a - b} \right)^3} = ?\).
Phương pháp giải:
1. Ta nhân đa thức với đa thức kết hợp với sử dụng hằng đẳng thức bình phương của một hiệu: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1.Ta có:
\(\begin{array}{l}{\left[ {a + \left( { - b} \right)} \right]^3} = {\left( {a - b} \right)^2}\left( {a - b} \right) = \left( {{a^2} - 2ab + {b^2}} \right)\left( {a - b} \right)\\ = {a^3} - 2{a^2}b + a{b^2} + 2a{b^2} - {a^2}b - {b^3}\\ = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\end{array}\)
2. \({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}.\)
Tính:
a) \({\left( {a - 3} \right)^3};\)
b) \({\left( {3u - 4v} \right)^3}.\)
Phương pháp giải:
Sử dụng hằng đẳng thức \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) thực hiện phép tính.
Lời giải chi tiết:
a)
\(\begin{array}{l}{\left( {a - 3} \right)^3} = {a^3} - 3.{a^2}.3 + 3.a{.3^2} - {3^3}\\ = {a^3} - 9{a^2} + 27a - 27\end{array}\)
b)
\(\begin{array}{l}{\left( {3u - 4v} \right)^3} = {\left( {3u} \right)^3} - 3.{\left( {3u} \right)^2}.4v + 3.3u.{\left( {4v} \right)^2} - {\left( {4v} \right)^2}\\ = 27{u^3} - 108{u^2}v + 144u{v^2} - 64{v^3}\end{array}\)
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right).\)
2. Hãy cho biết \({a^3} + {b^3} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. Ta có:
\(\left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right) = {a^3} - {a^2}b + a{b^2} + {a^2}b - a{b^2} + {b^3} = {a^3} + {b^3}.\)
2. \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\)
a) Viết \(8{a^3} + 27\) dưới dạng tích.
b) Viết \(\left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right)\) dưới dạng tổng.
Phương pháp giải:
Sử dụng hằng đẳng thức \({A^3} + {B^3} = \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right)\) thực hiện phép tính.
Lời giải chi tiết:
a) \(8{a^3} + 27 = {\left( {2a} \right)^3} + {3^3} = \left( {2a + 3} \right)\left( {4{a^2} - 6a + 9} \right)\)
b) \(\left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right) = {x^3} + 27\)
Cho \(a\) và \(b\) là hai số thực bất kì.
a) Thực hiện phép tính \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)
b) \({a^3} - {b^3} = ?\)
Phương pháp giải:
1. Ta nhân đa thức với đa thức: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
Lời giải chi tiết:
1. \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) = {a^3} + {a^2}b + a{b^2} - {a^2}b - a{b^2} - {b^3} = {a^3} - {b^3}.\)
2. \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)
a) Tính \(\left( {a - 4} \right)\left( {{a^2} + 4a + 16} \right).\)
b) Viết \(64{x^3} - 27{y^3}\) dưới dạng tích.
Phương pháp giải:
Sử dụng hằng đẳng thức \({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)\) thực hiện phép tính.
Lời giải chi tiết:
a) \(\left( {a - 4} \right)\left( {{a^2} + 4a + 16} \right) = {a^3} - {4^3} = {a^3} - 64\)
b) \(64{x^3} - 27{y^3} = {\left( {4x} \right)^3} - {\left( {3y} \right)^3} = \left( {4x - 3y} \right)\left( {16{x^2} - 12xy + 9{y^2}} \right)\)
Mục 2 của sách giáo khoa Toán 8 tập trung vào các kiến thức về hình học, cụ thể là các tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của các tứ giác này là vô cùng quan trọng để giải quyết các bài toán liên quan.
Dưới đây là phần giải chi tiết các bài tập trong mục 2, trang 19, 20, 21, 22, 23, 24 sách giáo khoa Toán 8. Chúng tôi sẽ trình bày từng bài tập một cách rõ ràng, dễ hiểu, kèm theo các hình vẽ minh họa (nếu cần) để giúp các em nắm bắt kiến thức một cách tốt nhất.
Đề bài: Cho hình bình hành ABCD. Gọi E là trung điểm của AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng: a) F là trung điểm của AC. b) AF = FC.
Giải:
Đề bài: Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng: a) OA = OB = OC = OD. b) Góc AOB = góc BOC = góc COD = góc DOA.
Giải:
(Giải thích chi tiết tương tự như bài 1, sử dụng tính chất của hình chữ nhật và các định lý liên quan)
Để học tốt môn Toán 8, các em cần:
Giaitoan.edu.vn hy vọng rằng với bộ giải chi tiết này, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán 8. Chúc các em thành công!