Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 78, 79 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 được trình bày rõ ràng, dễ hiểu, giúp các em tự tin hơn trong việc học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh nắm vững kiến thức Toán học, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong các kỳ thi.
1. Cho hình bình hành
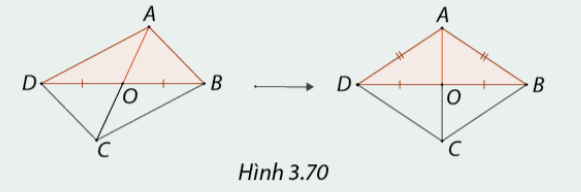
Phương pháp giải:
Dựa vào định nghĩa và tính chất của hình thoi để chứng minh.
Lời giải chi tiết:
Mà theo tính chất của hình bình hành thì các cạnh đối diện bằng nhau
→ \(AB = DC = AD = BC\)
Vì hình bình hành \(ABCD\) có bốn cạnh bằng nhau nên \(ABCD\) cũng là hình thoi.
Khi đó tứ giác \(ABCD\) là hình thoi vì có hai đường chéo \(AC \bot BD\) và chúng cắt nhau tại trung điểm của mỗi đường.
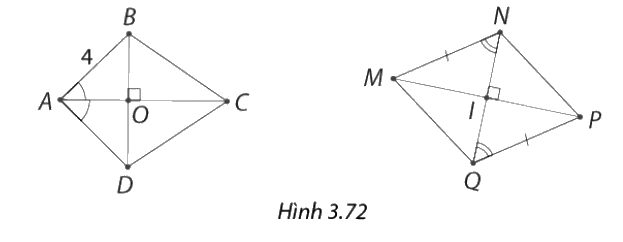
Tứ giác nào trong Hình 3.72 là hình thoi?
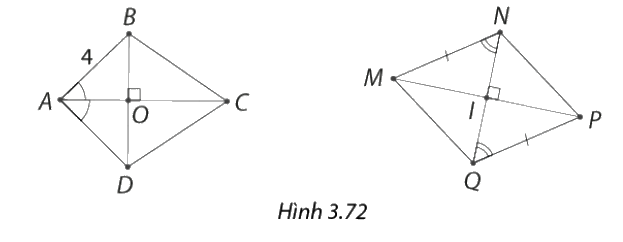
Phương pháp giải:
Dựa vào dấu hiệu nhận biết hình thoi để xác định tứ giác nào là hình thoi:
Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Lời giải chi tiết:
Tứ giác \(ABCD\) không phải là hình thoi bởi vì \(BD\) không đi qua trung điểm của \(AC\).
Xét tứ giác \(MNPQ\), ta có:
\(\widehat {NQP} = \widehat {MNQ}\)
Mà hai góc này ở vị trí đồng vị
→ \(MN//PQ\)
→ Tứ giác \(MNPQ\) là hình bình hành
Mà \(MP\) và \(NQ\) vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
→ Tứ giác \(MNPQ\) là hình thoi.
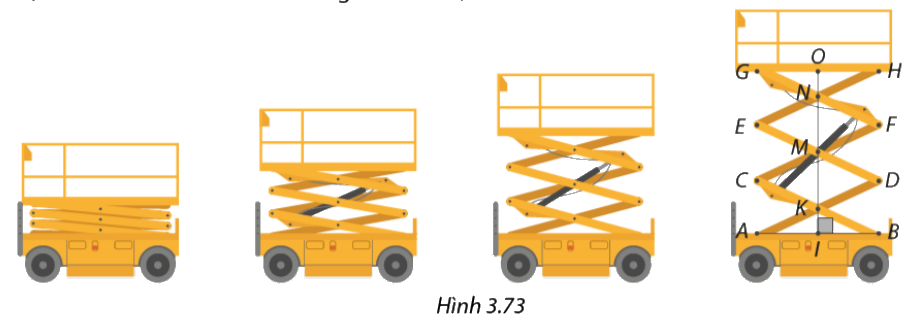
Hình 3.73 cho ta hình ảnh của một chiếc thang nâng thủy lực với khung nâng được lắp đặt từ các thanh giàn bằng nhau, gắn với nhau ở hai đầu và trung điểm mỗi thanh.
a) Tứ giác \(CKDM\) và tứ giác \(ABCD\) là hình gì?
b) Vì sao các đường thẳng \(AB,CD,EF\) và \(GH\) luôn song song với nhau? Vì sao các điểm \(I,K,M,N,O\) luôn thẳng hàng?
c) Tính chiều cao \(OI\) của thang khi \(AB = 1,6m\) và \(AD = 2m\)
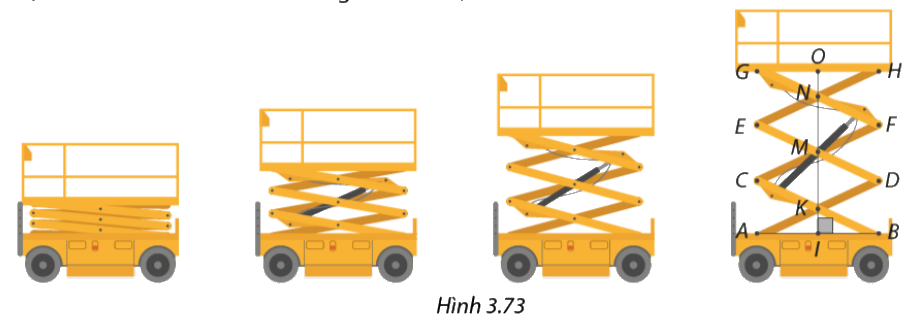
Phương pháp giải:
Dựa vào tính chất hình bình hành và tính chất hình chữ nhật để xác định.
c) Sử dụng định lí Pythagore để tính độ dài BD, từ đó tính OI.
Lời giải chi tiết:
a) Xét tứ giác \(CKDM\), ta có:
\(CM = MD = DK = KC\) (vì các thanh giàn bằng nhau và cắt nhau tại trung điểm)
Suy ra tứ giác \(CKDM\) là hình thoi.
Xét tứ giác \(ABCD\), ta có:
\(AD = CB\)
Mà \(AD\) và \(CB\) là hai đường chéo
nên \(ABCD\) là hình chữ nhật.
b) Các đường thẳng \(AB,CD,EF\) và \(GH\) luôn song song với nhau vì các đường thẳng này luôn bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Các điểm \(I,K,M,N,O\) luôn thẳng hàng vì các điểm này đều là giao điểm của hai đường chéo hình bình hành.
c) Vì ABCD là hình chữ nhật nên \(AB \bot BD\) do đó tam giác ABD vuông tại B.
Áp dụng định lí Pythagore vào tam giác ABD, ta có:
\(BD^2 = AD^2 - AB^2 = 2^2 – 1,6^2 = 1,44\) nên \(BD = 1,2 (m)\)
Ta dễ dàng chứng minh được tứ giác CDFE, EFHG là hình chữ nhật và BD = DF = FH
Khi đó BD = DF = HF = 1,2m
Mà OI = HB = BD + DF + FH = 1,2 + 1,2 + 1,2 = 3,6 (m)
Vậy OI = 3,6m.
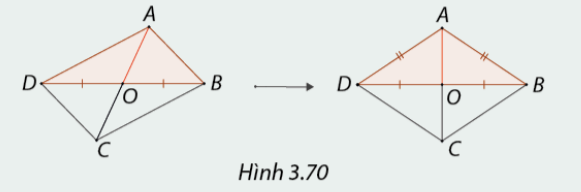
Phương pháp giải:
Dựa vào định nghĩa và tính chất của hình thoi để chứng minh.
Lời giải chi tiết:
Mà theo tính chất của hình bình hành thì các cạnh đối diện bằng nhau
→ \(AB = DC = AD = BC\)
Vì hình bình hành \(ABCD\) có bốn cạnh bằng nhau nên \(ABCD\) cũng là hình thoi.
Khi đó tứ giác \(ABCD\) là hình thoi vì có hai đường chéo \(AC \bot BD\) và chúng cắt nhau tại trung điểm của mỗi đường.
Tứ giác nào trong Hình 3.72 là hình thoi?
Phương pháp giải:
Dựa vào dấu hiệu nhận biết hình thoi để xác định tứ giác nào là hình thoi:
Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Lời giải chi tiết:
Tứ giác \(ABCD\) không phải là hình thoi bởi vì \(BD\) không đi qua trung điểm của \(AC\).
Xét tứ giác \(MNPQ\), ta có:
\(\widehat {NQP} = \widehat {MNQ}\)
Mà hai góc này ở vị trí đồng vị
→ \(MN//PQ\)
→ Tứ giác \(MNPQ\) là hình bình hành
Mà \(MP\) và \(NQ\) vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
→ Tứ giác \(MNPQ\) là hình thoi.
Hình 3.73 cho ta hình ảnh của một chiếc thang nâng thủy lực với khung nâng được lắp đặt từ các thanh giàn bằng nhau, gắn với nhau ở hai đầu và trung điểm mỗi thanh.
a) Tứ giác \(CKDM\) và tứ giác \(ABCD\) là hình gì?
b) Vì sao các đường thẳng \(AB,CD,EF\) và \(GH\) luôn song song với nhau? Vì sao các điểm \(I,K,M,N,O\) luôn thẳng hàng?
c) Tính chiều cao \(OI\) của thang khi \(AB = 1,6m\) và \(AD = 2m\)
Phương pháp giải:
Dựa vào tính chất hình bình hành và tính chất hình chữ nhật để xác định.
c) Sử dụng định lí Pythagore để tính độ dài BD, từ đó tính OI.
Lời giải chi tiết:
a) Xét tứ giác \(CKDM\), ta có:
\(CM = MD = DK = KC\) (vì các thanh giàn bằng nhau và cắt nhau tại trung điểm)
Suy ra tứ giác \(CKDM\) là hình thoi.
Xét tứ giác \(ABCD\), ta có:
\(AD = CB\)
Mà \(AD\) và \(CB\) là hai đường chéo
nên \(ABCD\) là hình chữ nhật.
b) Các đường thẳng \(AB,CD,EF\) và \(GH\) luôn song song với nhau vì các đường thẳng này luôn bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Các điểm \(I,K,M,N,O\) luôn thẳng hàng vì các điểm này đều là giao điểm của hai đường chéo hình bình hành.
c) Vì ABCD là hình chữ nhật nên \(AB \bot BD\) do đó tam giác ABD vuông tại B.
Áp dụng định lí Pythagore vào tam giác ABD, ta có:
\(BD^2 = AD^2 - AB^2 = 2^2 – 1,6^2 = 1,44\) nên \(BD = 1,2 (m)\)
Ta dễ dàng chứng minh được tứ giác CDFE, EFHG là hình chữ nhật và BD = DF = FH
Khi đó BD = DF = HF = 1,2m
Mà OI = HB = BD + DF + FH = 1,2 + 1,2 + 1,2 = 3,6 (m)
Vậy OI = 3,6m.
Mục 3 trong sách giáo khoa Toán 8 trang 78 và 79 thường tập trung vào một chủ đề cụ thể, ví dụ như các định lý liên quan đến hình bình hành, hình chữ nhật, hình thoi, hình vuông, hoặc các bài toán ứng dụng về các tứ giác đặc biệt này. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập trong mục này là rất quan trọng để học tốt môn Toán 8.
Thông thường, mục này sẽ bao gồm:
Dưới đây là một số dạng bài tập thường gặp trong mục 3 trang 78, 79 SGK Toán 8 và hướng dẫn giải:
Để chứng minh một tứ giác là một trong các hình đặc biệt trên, ta cần chứng minh các điều kiện tương ứng:
Để giải các bài toán này, ta cần sử dụng các định lý và tính chất của các hình đặc biệt. Ví dụ:
Các bài tập này thường yêu cầu học sinh vẽ hình, phân tích đề bài và vận dụng kiến thức đã học để giải quyết vấn đề. Ví dụ, bài toán về việc tính chiều dài của một con đường, chiều cao của một tòa nhà dựa trên các thông tin về hình học.
Bài tập: Cho hình chữ nhật ABCD, AB = 8cm, BC = 6cm. Tính độ dài đường chéo AC.
Giải:
Vì ABCD là hình chữ nhật nên góc ABC vuông. Áp dụng định lý Pitago vào tam giác ABC, ta có:
AC2 = AB2 + BC2 = 82 + 62 = 64 + 36 = 100
Suy ra AC = √100 = 10cm.
Để học tốt môn Toán 8, các em cần:
Hy vọng với bài giải chi tiết và hướng dẫn giải các dạng bài tập trên, các em học sinh sẽ tự tin hơn trong việc học tập và giải bài tập mục 3 trang 78, 79 SGK Toán 8. Chúc các em học tốt!