Chào mừng các em học sinh đến với bài giải chi tiết bài 6.34 trang 65 SGK Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
Trong Hình 6.88, để đo khoảng cách \(AB\) từ vị trí \(A\)
Đề bài
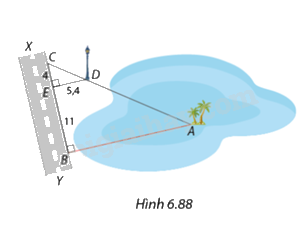
Trong Hình 6.88, để đo khoảng cách \(AB\) từ vị trí \(A\) giữa hồ nước đến đường \(XY\), Nam đi dọc đường đến vị trí C sao cho điểm A, C và chân cột đèn D thẳng hàng. Nam đo được khoảng cách từ D đến đường XY là \(DE = 5,4m\), ngoài ra \(CE = 4m\) và \(BE = 11m\). Tính khoảng cách \(AB\)
Phương pháp giải - Xem chi tiết
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết
Xét tam giác \(CED\) và tam giác \(CBA\), ta có:
\(\widehat C\) là góc chung
\(\widehat {CED} = \widehat {CBA} = 90^\circ \)
=> \(\Delta CED\)∽\(\Delta CBA\) (góc nhọn-góc vuông)
Ta có tỉ số đồng dạng:
\(\begin{array}{l}\frac{{CE}}{{CB}} = \frac{{ED}}{{BA}}\\\frac{4}{{4 + 11}} = \frac{{5,4}}{{BA}}\\ \Rightarrow BA = 20,25\end{array}\)
Vậy khoảng cách \(AB\) là 20,25 m.
Bài 6.34 trang 65 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần nắm vững các tính chất của hình chữ nhật, đặc biệt là mối quan hệ giữa các cạnh đối và các góc đối.
Đề bài yêu cầu chúng ta chứng minh một biểu thức đại số liên quan đến các cạnh của hình chữ nhật. Để làm được điều này, chúng ta cần phân tích đề bài một cách cẩn thận, xác định rõ các yếu tố đã cho và yếu tố cần chứng minh. Việc vẽ hình minh họa cũng rất quan trọng, giúp chúng ta hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
Đề bài: Cho hình chữ nhật ABCD. Gọi E là trung điểm của cạnh AD. Gọi F là trung điểm của cạnh BC. Chứng minh rằng: AE = BF.
Lời giải:
Trong hình chữ nhật ABCD, ta có: AD = BC (các cạnh đối bằng nhau).
Vì E là trung điểm của AD, nên AE = AD/2.
Vì F là trung điểm của BC, nên BF = BC/2.
Ta có: AE = AD/2 và BF = BC/2. Mà AD = BC (theo tính chất hình chữ nhật), nên AE = BF.
Vậy, AE = BF (đpcm).
Ngoài bài 6.34, còn rất nhiều bài tập tương tự liên quan đến hình chữ nhật và các tính chất của nó. Để giải quyết các bài tập này, học sinh cần:
Kiến thức về hình chữ nhật không chỉ dừng lại ở việc giải các bài tập trong sách giáo khoa mà còn có ứng dụng rất lớn trong thực tế. Ví dụ, trong xây dựng, hình chữ nhật được sử dụng để thiết kế các công trình như nhà cửa, phòng học, sân vận động,... Việc hiểu rõ về hình chữ nhật giúp chúng ta có thể tính toán diện tích, chu vi và các kích thước khác của các công trình này một cách chính xác.
Để củng cố kiến thức về bài 6.34 và các bài tập tương tự, các em có thể tự giải các bài tập sau:
Bài 6.34 trang 65 SGK Toán 8 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hình chữ nhật và các tính chất của nó. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn trong bài viết này, các em sẽ tự tin hơn trong việc giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.