Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 57, 58 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và giải quyết các bài tập một cách hiệu quả.
Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để các em hiểu sâu hơn về nội dung bài học.
Vẽ tam giác ABC có
Bạn Phát giải bài toán: “Tam giác ABC với \(AB = 5,AC = 13,BC = 12\) có phải là tam giác vuông hay không?” như sau:
Ta có:
\(A{B^2} + A{C^2} = {5^2} + {13^2} = 25 + 169 = 191;\)
\(B{C^2} = {12^2} = 144\)
Vì \(191 \ne 144\) nên \(A{B^2} + A{C^2} \ne B{C^2}\)
Vậy tam giác ABC không phải tam giác vuông.
Lời giải của Phát đúng hay sai? Vì sao?
Phương pháp giải:
Sử dụng định lí Pythagore đảo: Ta so sánh bình phương cạnh lớn nhất trong tam giác và tổng bình phương hai cạnh còn lại.
Lời giải chi tiết:
Ta so sánh bình phương cạnh lớn nhất trong tam giác và tổng bình phương hai cạnh còn lại.
Có \(A{C^2} = {13^2} = 169\) và \(A{B^2} + B{C^2} = {5^2} + {12^2} = 169 = A{C^2}\)
Vậy tam giác ABC là tam giác vuông tại B.
Lời giải của bạn Phát là sai.
Vẽ tam giác ABC có \(AB = 3cm,AC = 4cm,BC = 5cm.\)
a) So sánh \(B{C^2}\) và \(A{B^2} + A{C^2}.\)
b) Dùng thước đo góc để xác định số đo góc \(BAC.\)
Phương pháp giải:
a) Dựa vào số liệu đề bài thực hiện phép tính
b) Dùng thước đo góc để xác định số đo góc \(BAC.\)
Lời giải chi tiết:
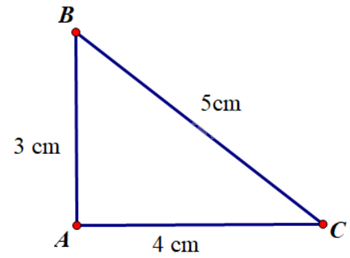
a) Ta có \(B{C^2} = {5^2} = 25\) và \(A{B^2} + A{C^2} = {4^2} + {3^2} = 25\)
Vậy \(B{C^2} = A{C^2} + A{B^2}\)
b) Sử dụng thước đo góc, ta đo được số đo góc \(BAC\) bằng \(90^\circ \).
Bạn Phát giải bài toán: “Tam giác ABC với \(AB = 5,AC = 13,BC = 12\) có phải là tam giác vuông hay không?” như sau:
Ta có:
\(A{B^2} + A{C^2} = {5^2} + {13^2} = 25 + 169 = 191;\)
\(B{C^2} = {12^2} = 144\)
Vì \(191 \ne 144\) nên \(A{B^2} + A{C^2} \ne B{C^2}\)
Vậy tam giác ABC không phải tam giác vuông.
Lời giải của Phát đúng hay sai? Vì sao?
Phương pháp giải:
Sử dụng định lí Pythagore đảo: Ta so sánh bình phương cạnh lớn nhất trong tam giác và tổng bình phương hai cạnh còn lại.
Lời giải chi tiết:
Ta so sánh bình phương cạnh lớn nhất trong tam giác và tổng bình phương hai cạnh còn lại.
Có \(A{C^2} = {13^2} = 169\) và \(A{B^2} + B{C^2} = {5^2} + {12^2} = 169 = A{C^2}\)
Vậy tam giác ABC là tam giác vuông tại B.
Lời giải của bạn Phát là sai.
Vẽ tam giác ABC có \(AB = 3cm,AC = 4cm,BC = 5cm.\)
a) So sánh \(B{C^2}\) và \(A{B^2} + A{C^2}.\)
b) Dùng thước đo góc để xác định số đo góc \(BAC.\)
Phương pháp giải:
a) Dựa vào số liệu đề bài thực hiện phép tính
b) Dùng thước đo góc để xác định số đo góc \(BAC.\)
Lời giải chi tiết:
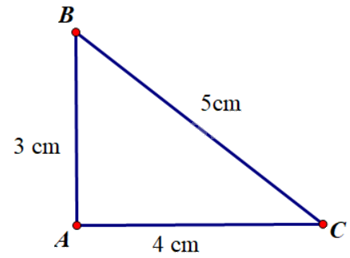
a) Ta có \(B{C^2} = {5^2} = 25\) và \(A{B^2} + A{C^2} = {4^2} + {3^2} = 25\)
Vậy \(B{C^2} = A{C^2} + A{B^2}\)
b) Sử dụng thước đo góc, ta đo được số đo góc \(BAC\) bằng \(90^\circ \).
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi và hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của chúng là vô cùng quan trọng để giải quyết các bài tập liên quan.
Mục 2 thường bao gồm các nội dung sau:
Để giải tốt các bài tập liên quan đến Mục 2, các em cần:
Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = FC.
Lời giải:
Các em cần chú ý:
Kiến thức về tứ giác có ứng dụng rộng rãi trong thực tế, ví dụ như:
Hy vọng bài viết này sẽ giúp các em hiểu rõ hơn về Mục 2 trang 57, 58 SGK Toán 8 và giải quyết các bài tập một cách hiệu quả. Chúc các em học tập tốt!