Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 trong sách giáo khoa. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài toán phức tạp.
Với mục tiêu hỗ trợ học sinh nắm vững kiến thức, chúng tôi đã biên soạn bộ giải đáp đầy đủ cho trang 53, 54, 55 SGK Toán 8.
Hãy cùng khám phá và chinh phục những bài toán Toán 8 một cách hiệu quả nhất!
Xét tam giác \(ABC\) và tam giác \(A'B'C'\)
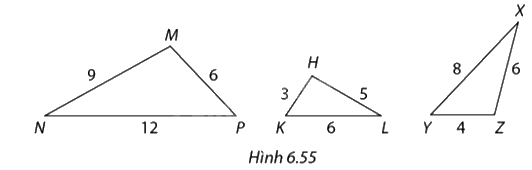
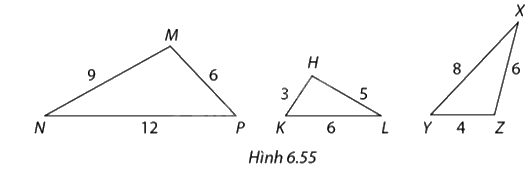
Chỉ ra các cặp tam giác đồng dạng trong Hình 6.55. Viết kí hiệu về sự đồng dạng của chúng và xác định tỉ số đồng dạng.
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Ta có: \(\Delta MNP\)∽\(\Delta XYZ\):
\(\begin{array}{l}\frac{{MP}}{{YZ}} = \frac{6}{4} = \frac{3}{2}\\\frac{{MN}}{{ZX}} = \frac{9}{6} = \frac{3}{2}\\\frac{{NP}}{{XY}} = \frac{{12}}{8} = \frac{3}{2}\end{array}\)
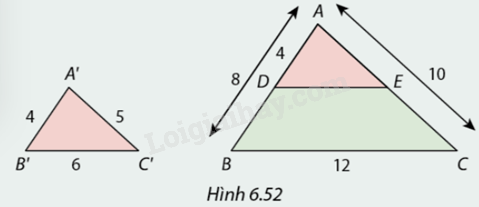
Xét tam giác \(ABC\) và tam giác \(A'B'C'\) có độ dài cạnh như trong hình 6.52.
Đường thẳng \(DE\) song song với cạnh \(BC.\)
1. Vì sao \(\Delta ADE∽\Delta ABC?\)
2. Tính độ dài \(AE\) và \(DE\). Vì sao \(\Delta ADE = \Delta A'B'C'?\)
Em có kết luận gì về \(\Delta \,ABC\)và \(\Delta A'B'C'?\)
Phương pháp giải:
Dựa vào định nghĩa và định lí hai tam giác đồng dạng để chứng minh \(\Delta ADE∽\Delta ABC\).
Sau đó tính độ dài \(AE\) và \(DE\).
Lời giải chi tiết:
1. Xét tam giác \(ADE\) và tam giác \(ABC\), có:
Đường thẳng DE cắt AB tại D, cắt AC tại E
Mà \(DE//BC\).
Áp dụng định lí hai tam giác đồng dạng suy ra \(\Delta ADE\)∽\(\Delta ABC\).
2. Vì \(\Delta ADE\)∽\(\Delta ABC\).
\(\begin{array}{l} = > \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\\ \Leftrightarrow \frac{4}{8} = \frac{{AE}}{{10}} = \frac{{DE}}{{12}}\\ \Rightarrow AE = 5;DE = 6\end{array}\)
Xét tam giác \(A'B'C'\) và tam giác \(ADC\), ta có:
\(\begin{array}{l}A'B' = AD = 4\\A'C' = AE = 5\\B'C' = DE = 6\end{array}\)
=> \(\Delta ADE = \Delta A'B'C'\)
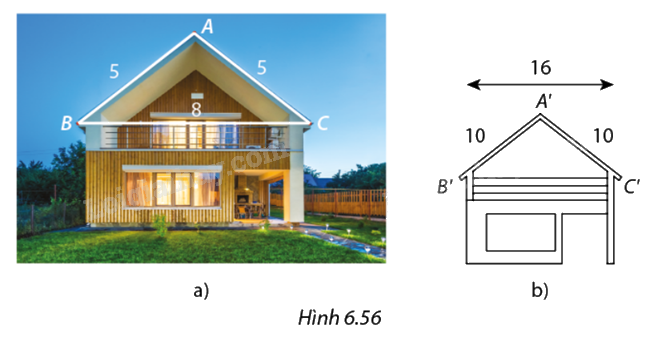
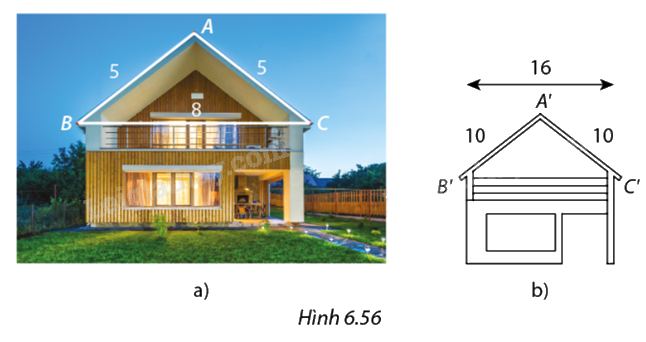
Trên bản vẽ thiết kế mặt tiền ngôi nhà ở Hình 5.65b, khoảng cách thực tế giữa các đỉnh \(A',B',C'\) của mái nhà là \(A'B' = A'C' = 10\,cm,B'C' = 16\,cm.\) Trên thực tế, mái nhà được xây dựng có kích thước \(AB = AC = 5\,m\) và \(BC = 8\,m\) (Hình 5.56a). Hỏi mặt tiền của mái nhà có được xây dựng đúng với hình dạng như được thiết kế không?
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Để mặt tiền của mái nhà được xây đúng với hình dạng như được thiết kế thì:
\(\Delta ABC\)∽\(\Delta A'B'C'\)
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\)
Mà
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{AC}}{{A'C'}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{BC}}{{B'C'}} = \frac{8}{{16}} = \frac{1}{2}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\end{array}\)
Vậy mặt tiền của mái nhà được xây đúng với hình dạng như được thiết kế.
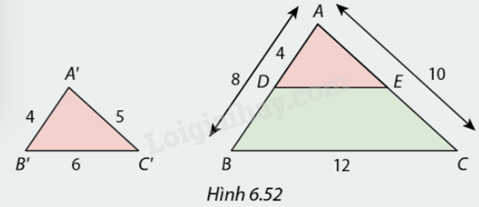
Xét tam giác \(ABC\) và tam giác \(A'B'C'\) có độ dài cạnh như trong hình 6.52.
Đường thẳng \(DE\) song song với cạnh \(BC.\)
1. Vì sao \(\Delta ADE∽\Delta ABC?\)
2. Tính độ dài \(AE\) và \(DE\). Vì sao \(\Delta ADE = \Delta A'B'C'?\)
Em có kết luận gì về \(\Delta \,ABC\)và \(\Delta A'B'C'?\)
Phương pháp giải:
Dựa vào định nghĩa và định lí hai tam giác đồng dạng để chứng minh \(\Delta ADE∽\Delta ABC\).
Sau đó tính độ dài \(AE\) và \(DE\).
Lời giải chi tiết:
1. Xét tam giác \(ADE\) và tam giác \(ABC\), có:
Đường thẳng DE cắt AB tại D, cắt AC tại E
Mà \(DE//BC\).
Áp dụng định lí hai tam giác đồng dạng suy ra \(\Delta ADE\)∽\(\Delta ABC\).
2. Vì \(\Delta ADE\)∽\(\Delta ABC\).
\(\begin{array}{l} = > \frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\\ \Leftrightarrow \frac{4}{8} = \frac{{AE}}{{10}} = \frac{{DE}}{{12}}\\ \Rightarrow AE = 5;DE = 6\end{array}\)
Xét tam giác \(A'B'C'\) và tam giác \(ADC\), ta có:
\(\begin{array}{l}A'B' = AD = 4\\A'C' = AE = 5\\B'C' = DE = 6\end{array}\)
=> \(\Delta ADE = \Delta A'B'C'\)
Chỉ ra các cặp tam giác đồng dạng trong Hình 6.55. Viết kí hiệu về sự đồng dạng của chúng và xác định tỉ số đồng dạng.
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Ta có: \(\Delta MNP\)∽\(\Delta XYZ\):
\(\begin{array}{l}\frac{{MP}}{{YZ}} = \frac{6}{4} = \frac{3}{2}\\\frac{{MN}}{{ZX}} = \frac{9}{6} = \frac{3}{2}\\\frac{{NP}}{{XY}} = \frac{{12}}{8} = \frac{3}{2}\end{array}\)
Trên bản vẽ thiết kế mặt tiền ngôi nhà ở Hình 5.65b, khoảng cách thực tế giữa các đỉnh \(A',B',C'\) của mái nhà là \(A'B' = A'C' = 10\,cm,B'C' = 16\,cm.\) Trên thực tế, mái nhà được xây dựng có kích thước \(AB = AC = 5\,m\) và \(BC = 8\,m\) (Hình 5.56a). Hỏi mặt tiền của mái nhà có được xây dựng đúng với hình dạng như được thiết kế không?
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Để mặt tiền của mái nhà được xây đúng với hình dạng như được thiết kế thì:
\(\Delta ABC\)∽\(\Delta A'B'C'\)
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\)
Mà
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{AC}}{{A'C'}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{BC}}{{B'C'}} = \frac{8}{{16}} = \frac{1}{2}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\end{array}\)
Vậy mặt tiền của mái nhà được xây đúng với hình dạng như được thiết kế.
Chương trình Toán 8 đóng vai trò quan trọng trong việc xây dựng nền tảng toán học vững chắc cho học sinh. Trang 53, 54, 55 của sách giáo khoa Toán 8 thường chứa các bài tập liên quan đến các chủ đề như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, bất phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn, và các ứng dụng thực tế của chúng. Việc nắm vững kiến thức và kỹ năng giải các bài tập này là điều cần thiết để học sinh có thể tiếp thu tốt các kiến thức nâng cao hơn trong các lớp học tiếp theo.
Trang 53 SGK Toán 8 thường tập trung vào việc ôn tập và củng cố kiến thức về các phép toán với đa thức. Các bài tập thường yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia đa thức, đồng thời áp dụng các quy tắc về dấu và bậc của đa thức. Để giải các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đa thức, bao gồm định nghĩa, các loại đa thức, và các phép toán với đa thức.
Trang 54 SGK Toán 8 thường giới thiệu về phân thức đại số. Các bài tập thường yêu cầu học sinh nhận biết, so sánh, và thực hiện các phép toán với phân thức đại số. Để giải các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về phân thức đại số, bao gồm định nghĩa, điều kiện xác định, và các phép toán với phân thức đại số.
Trang 55 SGK Toán 8 thường tập trung vào việc giải phương trình bậc nhất một ẩn. Các bài tập thường yêu cầu học sinh tìm nghiệm của phương trình, đồng thời kiểm tra lại nghiệm bằng cách thay vào phương trình ban đầu. Để giải các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về phương trình bậc nhất một ẩn, bao gồm định nghĩa, các phép biến đổi tương đương, và phương pháp giải phương trình.
Giaitoan.edu.vn cung cấp:
Việc giải bài tập Toán 8 trang 53, 54, 55 SGK là một bước quan trọng trong quá trình học tập của học sinh. Hy vọng rằng với sự hỗ trợ của giaitoan.edu.vn, các em sẽ tự tin hơn trong việc chinh phục môn Toán và đạt được kết quả tốt nhất.