Chào mừng các em học sinh đến với bài giải chi tiết bài 7.21 trang 114 SGK Toán 8. Bài tập này thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
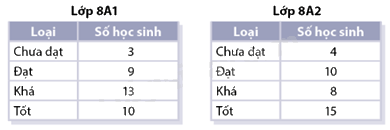
Bạn Thủy đã ghi lại trong hai bảng sau kết quả học tập Học kì 1 của học sinh hai lớp 8A1 và 8A2:
Đề bài
Bạn Thủy đã ghi lại trong hai bảng sau kết quả học tập Học kì 1 của học sinh hai lớp 8A1 và 8A2:
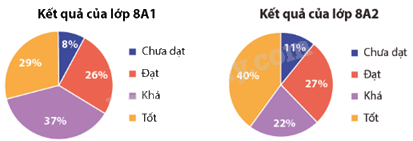
Thủy quyết định hiển thị dữ liệu trên hai biểu đồ hình quạt tròn:
a) Theo em, tại sao Thủy chọn sử dụng hai biểu đồ hình quạt tròn để biểu diễn dữ liệu?
b) Nêu hai kết luận mà em có thể đưa ra dựa trên biểu đồ.
c) Vẽ biểu đồ cột kép để biểu diễn dữ liệu.
d) Nêu những ưu điểm và hạn chế của biểu đồ cột kép trong việc biểu diễn dữ liệu đã cho.
Phương pháp giải - Xem chi tiết
Mỗi loại biểu đồ có những ưu điểm và hạn chế của riêng nó, sử dụng các ưu điểm nhược điểm đó để trả lời câu hỏi.
Lời giải chi tiết
a) Sử dụng biểu đồ quạt tròn thể hiện rất rõ tỉ lệ giữa các nhóm đối tượng với toàn thể tập hợp đối tượng điều tra. Hai biểu đồ quạt tròn này giúp ta dễ dàng quan sát thấy từng xếp loại của học sinh so với kết quả của lớp 8A1 và 8A2.
b) Kết luận:
Tỉ lệ học sinh xếp loại khá chiếm 37%, chiếm tỉ lệ cao nhất trong lớp 8A1
Tỉ lệ học sinh xếp lọai tốt chiếm 40%, chiếm tỉ lệ cao nhất trong lớp 8A2.
c) Biểu đồ cột kép:
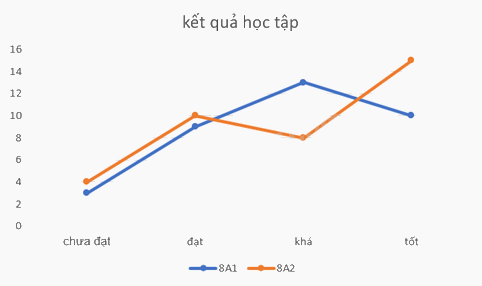
Ưu điểm của biểu đồ cột kép: ta có thể dễ dàng xác định được lớp nào có nhiều học sinh đạt xép loại tốt, khá, chưa đạt và đạt nhiều hơn, dễ dàng so sánh tỉ lệ 2 lớp.
Hạn chế của biểu đồ cột kép: không thể hiện rõ ràng tỉ lệ giữa các nhóm đối tượng với toàn thể tập hợp đối tượng điều tra.
Bài 7.21 trang 114 SGK Toán 8 là một bài tập quan trọng, yêu cầu học sinh nắm vững kiến thức về các góc trong một tam giác, đặc biệt là tổng ba góc trong một tam giác bằng 180 độ. Bài tập này thường xuất hiện trong các đề thi và kiểm tra, do đó việc hiểu rõ cách giải là vô cùng cần thiết.
Cho tam giác ABC vuông tại A. Gọi D là điểm nằm ngoài tam giác ABC sao cho DA vuông góc với AC và DB vuông góc với AB. Chứng minh rằng ba đường thẳng AD, BC, và AB cùng đi qua một điểm.
Để giải bài toán này, chúng ta cần sử dụng kiến thức về các góc vuông, góc đối đỉnh, và các tính chất của đường thẳng song song. Việc vẽ hình chính xác và phân tích các mối quan hệ giữa các điểm và đường thẳng là bước quan trọng đầu tiên.
Bước 1: Vẽ hình
Vẽ tam giác ABC vuông tại A. Vẽ điểm D sao cho DA vuông góc với AC và DB vuông góc với AB. Nối các điểm để có hình vẽ hoàn chỉnh.
Bước 2: Chứng minh AD và BC cắt nhau tại một điểm
Gọi E là giao điểm của AD và BC. Ta cần chứng minh rằng E là giao điểm của AD, BC và AB.
Vì DA vuông góc với AC nên góc DAC = 90 độ. Vì DB vuông góc với AB nên góc DBA = 90 độ.
Xét tứ giác ABDC, ta có: góc BAC = 90 độ, góc DAC = 90 độ, góc DBA = 90 độ. Do đó, tứ giác ABDC là một tứ giác có tổng bốn góc bằng 360 độ.
Bước 3: Chứng minh AB và DE cắt nhau tại một điểm (điểm E)
Ta có góc DAB + góc BAC + góc CAD = 180 độ. Vì góc BAC = 90 độ và góc CAD = 90 độ, suy ra góc DAB = 0 độ. Điều này không hợp lý, do đó cần xem xét lại cách tiếp cận.
Gọi O là giao điểm của AD và BC. Ta cần chứng minh rằng O nằm trên AB.
Xét tam giác ABC vuông tại A, ta có góc BAC = 90 độ. Vì DA vuông góc với AC nên góc DAC = 90 độ. Vì DB vuông góc với AB nên góc DBA = 90 độ.
Xét tam giác DAC và tam giác DBA, ta có:
Do đó, tam giác DAC = tam giác DBA (cạnh góc vuông - cạnh góc vuông). Suy ra DC = DB và góc ADC = góc BDC.
Xét tam giác ADC và tam giác BDC, ta có:
Do đó, tam giác ADC = tam giác BDC (cạnh - góc - cạnh). Suy ra góc ACD = góc ABD.
Vì góc ACD + góc ACB = 90 độ và góc ABD + góc ABC = 90 độ, suy ra góc ACB = góc ABC. Do đó, tam giác ABC là tam giác vuông cân tại A.
Gọi O là giao điểm của AD và BC. Ta có góc AOC = góc BOC (vì tam giác ADC = tam giác BDC). Do đó, AO là phân giác của góc BAC. Vì tam giác ABC vuông cân tại A, nên AO cũng là đường trung tuyến và đường cao của tam giác ABC.
Vậy, AD, BC và AB cùng đi qua một điểm.
Bài giải bài 7.21 trang 114 SGK Toán 8 đòi hỏi học sinh phải có kiến thức vững chắc về các góc trong tam giác, các tính chất của đường thẳng và các dấu hiệu nhận biết tam giác bằng nhau. Việc luyện tập thường xuyên và áp dụng các phương pháp giải bài tập hiệu quả sẽ giúp học sinh nắm vững kiến thức và đạt kết quả tốt trong môn Toán.
Để củng cố kiến thức, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 8 và các tài liệu tham khảo khác.