Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 66, 67 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, giảm bớt gánh nặng trong quá trình học tập môn Toán.
Vẽ tam giác \(ABC\) và một điểm \(O\) bất kì.
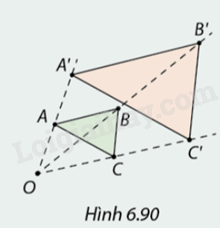
Vẽ tam giác \(ABC\) và một điểm \(O\) bất kì. Trên các tia \(OA,OB,OC,\) chọn các điểm \(A',B',C'\) sao cho \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 2\) (Hình 6.90).
a) Các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\) bằng bao nhiêu? Các cặp cạnh \(A'B'\) và \(AB,A'C'\) và \(AC,B'C'\) và \(BC\) có song song không?
b) Em có nhận xét gì về tam giác \(ABC\) và tam giác \(A'B'C'\)?
Phương pháp giải:
Xác định các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\), dựa vào tính chất đường trung bình của tam giác xác định các cạnh \(A'B'\) và \(AB,A'C'\) và \(AC,B'C'\) và \(BC\) có song song không. Sau đó nhận xét về tam giác \(ABC\) và tam giác \(A'B'C'\).
Lời giải chi tiết:
a) Xét tam giác \(OA'C'\), ta có:
\(\frac{{OA'}}{{OC'}} = 2\)
=> A là trung điểm của \(OA'\)
\(\frac{{OC'}}{{OC}} = 2\)
=> C là trung điểm của \(OC'\).
=> AC là đường trung bình của tam giác \(OA'C'\).
Áp dụng tính chất đường trung bình của tam giác ta có: \(\frac{{AC}}{{A'C'}} = \frac{1}{2}\).
Chứng minh tương tự với tam giác \(OA'B';OB'C'\)
Ta được tỉ số: \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\).
Các cặp cạnh \(AB//A'B';BC//B'C';AC//A'C'\).
b) Vì \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\), ta được \(\Delta ABC\) ∽ \(\Delta A'B'C'\) (cạnh-cạnh-cạnh).
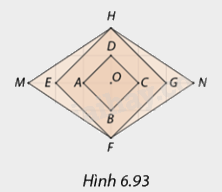
Trong Hình 6.93, tứ giác nào là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) và theo tỉ số là bao nhiêu?
Phương pháp giải:
Dựa vào tỉ số bằng nhau xác định tứ giác nào là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) và tỉ số là bao nhiêu.
Lời giải chi tiết:
Tứ giác \(EHGD\) là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) với tỉ số là:
\(\frac{{OE}}{{OA}} = \frac{{OH}}{{OD}} = \frac{{ON}}{{OG}} = \frac{{OF}}{{OB}} = 2\).
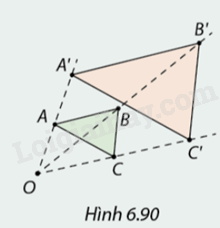
Vẽ tam giác \(ABC\) và một điểm \(O\) bất kì. Trên các tia \(OA,OB,OC,\) chọn các điểm \(A',B',C'\) sao cho \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{{OC'}}{{OC}} = 2\) (Hình 6.90).
a) Các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\) bằng bao nhiêu? Các cặp cạnh \(A'B'\) và \(AB,A'C'\) và \(AC,B'C'\) và \(BC\) có song song không?
b) Em có nhận xét gì về tam giác \(ABC\) và tam giác \(A'B'C'\)?
Phương pháp giải:
Xác định các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\), dựa vào tính chất đường trung bình của tam giác xác định các cạnh \(A'B'\) và \(AB,A'C'\) và \(AC,B'C'\) và \(BC\) có song song không. Sau đó nhận xét về tam giác \(ABC\) và tam giác \(A'B'C'\).
Lời giải chi tiết:
a) Xét tam giác \(OA'C'\), ta có:
\(\frac{{OA'}}{{OC'}} = 2\)
=> A là trung điểm của \(OA'\)
\(\frac{{OC'}}{{OC}} = 2\)
=> C là trung điểm của \(OC'\).
=> AC là đường trung bình của tam giác \(OA'C'\).
Áp dụng tính chất đường trung bình của tam giác ta có: \(\frac{{AC}}{{A'C'}} = \frac{1}{2}\).
Chứng minh tương tự với tam giác \(OA'B';OB'C'\)
Ta được tỉ số: \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\).
Các cặp cạnh \(AB//A'B';BC//B'C';AC//A'C'\).
b) Vì \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\), ta được \(\Delta ABC\) ∽ \(\Delta A'B'C'\) (cạnh-cạnh-cạnh).
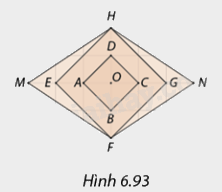
Trong Hình 6.93, tứ giác nào là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) và theo tỉ số là bao nhiêu?
Phương pháp giải:
Dựa vào tỉ số bằng nhau xác định tứ giác nào là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) và tỉ số là bao nhiêu.
Lời giải chi tiết:
Tứ giác \(EHGD\) là hình đồng dạng phối cảnh tâm \(O\) của hình vuông \(ABCD\) với tỉ số là:
\(\frac{{OE}}{{OA}} = \frac{{OH}}{{OD}} = \frac{{ON}}{{OG}} = \frac{{OF}}{{OB}} = 2\).
Mục 1 trang 66, 67 SGK Toán 8 thường chứa các bài tập về các kiến thức cơ bản của chương trình đại số hoặc hình học. Để giải quyết các bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và định lý đã học. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 1, giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Thông thường, mục 1 trang 66, 67 sẽ tập trung vào một trong các chủ đề sau:
Đề bài: Thu gọn đa thức sau: A = 3x2 + 2xy - x2 + 5xy - 3y2
Lời giải:
Đề bài: Phân tích đa thức sau thành nhân tử: B = x2 - 4x + 4
Lời giải:
Áp dụng hằng đẳng thức (a - b)2 = a2 - 2ab + b2, ta có:
B = x2 - 2.2.x + 22 = (x - 2)2
Đề bài: Cho hình bình hành ABCD. Gọi E là trung điểm của AB. Chứng minh rằng DE là phân giác của góc ADC.
Lời giải:
Vì ABCD là hình bình hành nên AB // CD và AD // BC. Do đó, góc DAB = góc BCD và góc ADC = góc ABC.
Vì E là trung điểm của AB nên AE = EB. Xét tam giác ADE và tam giác BCE, ta có:
Do đó, tam giác ADE = tam giác BCE (c.g.c). Suy ra góc ADE = góc BCE.
Vì góc ADC = góc ABC và góc ABC = góc BCE + góc ABE, nên góc ADC = góc BCE + góc ABE.
Mà góc ADE = góc BCE, nên góc EDC = góc ADC - góc ADE = góc BCE + góc ABE - góc BCE = góc ABE.
Vậy DE là phân giác của góc ADC.
Để học tốt môn Toán 8, các em cần:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng bài giải chi tiết này sẽ giúp các em học tốt môn Toán 8. Chúc các em thành công!