Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 trong sách giáo khoa. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ học sinh học tập hiệu quả, chúng tôi đã biên soạn bộ giải đáp đầy đủ cho trang 56 và 57 SGK Toán 8, giúp bạn giải quyết mọi vấn đề một cách nhanh chóng và chính xác.
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng tờ giấy có
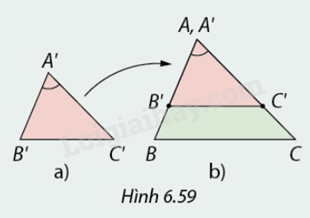
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng tờ giấy có \(\widehat {A'} = \widehat A\) và \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}.\) Xếp \(\Delta A'B'C'\) và \(\Delta ABC\) sao cho cạnh \(A'B'\) chồng lên cạnh \(AB\) và cạnh \(A'C'\) chồng lên cạnh \(AC\) như Hình 6.59.
1. Vì sao trong Hình \(6.59b\) cạnh \(B'C'\) song song với cạnh \(BC?\)
2. Em có kết luận gì về \(\Delta A'B'C'\) và \(\Delta ABC\)?
Phương pháp giải:
Dựa vào định lí Thales để chứng minh cạnh \(B'C'\) song song với cạnh \(BC\).
Lời giải chi tiết:
1. Ta có: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
\(B'C'\) cắt \(AB\) và \(AC\) lần lượt tại \(B'\) và \(C'\)
=> \(B'C'//BC\) (áp dụng định lí Thales)
2. Theo định lí: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Ta được: \(\Delta ABC\) ∽ \(\Delta A'B'C'\).
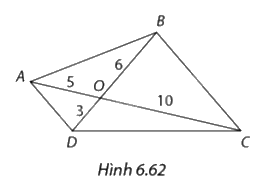
Khẳng định nào sau đây đúng với các tam giác trong Hình 6.22?
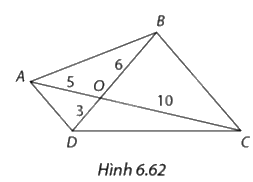
a) \(\Delta AOD \backsim \Delta COB;\)
b) \(\Delta AOB \backsim \Delta DOC.\)
Phương pháp giải:
Áp dụng trường hợp đồng dạng cạnh góc cạnh:
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng.
Lời giải chi tiết:
a) Xét tam giác \(AOD\) và tam giác \(COB\), ta có:
\(\begin{array}{l}\frac{{AO}}{{CO}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{DO}}{{BO}} = \frac{3}{6} = \frac{1}{2}\\ = > \frac{{AO}}{{CO}} = \frac{{DO}}{{BO}} = \frac{1}{2}\end{array}\)
Mà \(\widehat {AOD} = \widehat {COB}\) (hai góc đối đỉnh)
=> \(\Delta AOD\) ∽ \(\Delta COB\) (c-g-c)
b) Xét tam giác \(AOB\) và tam giác \(DOC\), ta có:
\(\begin{array}{l}\frac{{AO}}{{CO}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{DO}}{{BO}} = \frac{3}{6} = \frac{1}{2}\\ = > \frac{{AO}}{{CO}} = \frac{{DO}}{{BO}} = \frac{1}{2}\end{array}\)
Mà \(\widehat {AOB} = \widehat {DOC}\) (hai góc đối đỉnh)
=>\(\Delta AOB\) ∽ \(\Delta DOC\) (c-g-c)
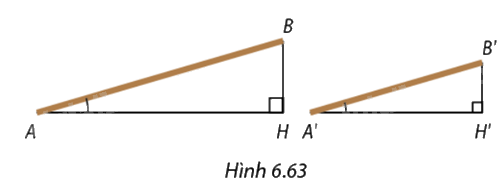
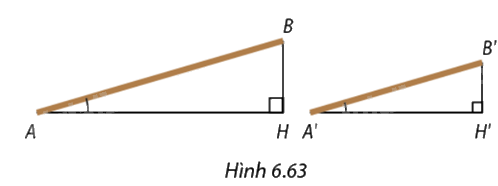
Trong Hình 6.63, hai đường ram dốc \(AB\) và \(A'B'\) có cùng tỉ số chiều cao và chiều dài \(\frac{{BH}}{{AH}} = \frac{{B'H'}}{{A'H'}}.\) Em hãy giải thích vì sao \(\widehat A = \widehat {A'}.\)
Phương pháp giải:
Áp dụng trường hợp đồng dạng cạnh góc cạnh:
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng.
Lời giải chi tiết:
Xét \(\Delta ABH\) và \(\Delta A'B'H'\), ta có:
\(\begin{array}{l}\frac{{BH}}{{AH}} = \frac{{B'H'}}{{A'H'}}\\ = > \frac{{BH}}{{B'H'}} = \frac{{AH}}{{A'H'}}\end{array}\)
Mà \(AB\) và \(A'B'\) có cùng tỉ số chiều cao
\(\widehat {AHB} = \widehat {A'H'B'} = 90^\circ \)
=>\(\Delta ABH\) ∽ \(\Delta A'B'H'\) (c-g-c)
=> \(\widehat A = \widehat {A'}\) (cặp góc tương ứng)
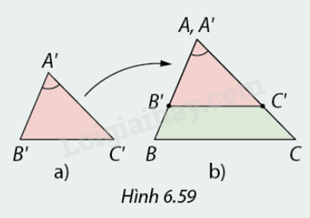
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng tờ giấy có \(\widehat {A'} = \widehat A\) và \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}.\) Xếp \(\Delta A'B'C'\) và \(\Delta ABC\) sao cho cạnh \(A'B'\) chồng lên cạnh \(AB\) và cạnh \(A'C'\) chồng lên cạnh \(AC\) như Hình 6.59.
1. Vì sao trong Hình \(6.59b\) cạnh \(B'C'\) song song với cạnh \(BC?\)
2. Em có kết luận gì về \(\Delta A'B'C'\) và \(\Delta ABC\)?
Phương pháp giải:
Dựa vào định lí Thales để chứng minh cạnh \(B'C'\) song song với cạnh \(BC\).
Lời giải chi tiết:
1. Ta có: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
\(B'C'\) cắt \(AB\) và \(AC\) lần lượt tại \(B'\) và \(C'\)
=> \(B'C'//BC\) (áp dụng định lí Thales)
2. Theo định lí: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Ta được: \(\Delta ABC\) ∽ \(\Delta A'B'C'\).
Khẳng định nào sau đây đúng với các tam giác trong Hình 6.22?
a) \(\Delta AOD \backsim \Delta COB;\)
b) \(\Delta AOB \backsim \Delta DOC.\)
Phương pháp giải:
Áp dụng trường hợp đồng dạng cạnh góc cạnh:
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng.
Lời giải chi tiết:
a) Xét tam giác \(AOD\) và tam giác \(COB\), ta có:
\(\begin{array}{l}\frac{{AO}}{{CO}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{DO}}{{BO}} = \frac{3}{6} = \frac{1}{2}\\ = > \frac{{AO}}{{CO}} = \frac{{DO}}{{BO}} = \frac{1}{2}\end{array}\)
Mà \(\widehat {AOD} = \widehat {COB}\) (hai góc đối đỉnh)
=> \(\Delta AOD\) ∽ \(\Delta COB\) (c-g-c)
b) Xét tam giác \(AOB\) và tam giác \(DOC\), ta có:
\(\begin{array}{l}\frac{{AO}}{{CO}} = \frac{5}{{10}} = \frac{1}{2}\\\frac{{DO}}{{BO}} = \frac{3}{6} = \frac{1}{2}\\ = > \frac{{AO}}{{CO}} = \frac{{DO}}{{BO}} = \frac{1}{2}\end{array}\)
Mà \(\widehat {AOB} = \widehat {DOC}\) (hai góc đối đỉnh)
=>\(\Delta AOB\) ∽ \(\Delta DOC\) (c-g-c)
Trong Hình 6.63, hai đường ram dốc \(AB\) và \(A'B'\) có cùng tỉ số chiều cao và chiều dài \(\frac{{BH}}{{AH}} = \frac{{B'H'}}{{A'H'}}.\) Em hãy giải thích vì sao \(\widehat A = \widehat {A'}.\)
Phương pháp giải:
Áp dụng trường hợp đồng dạng cạnh góc cạnh:
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng.
Lời giải chi tiết:
Xét \(\Delta ABH\) và \(\Delta A'B'H'\), ta có:
\(\begin{array}{l}\frac{{BH}}{{AH}} = \frac{{B'H'}}{{A'H'}}\\ = > \frac{{BH}}{{B'H'}} = \frac{{AH}}{{A'H'}}\end{array}\)
Mà \(AB\) và \(A'B'\) có cùng tỉ số chiều cao
\(\widehat {AHB} = \widehat {A'H'B'} = 90^\circ \)
=>\(\Delta ABH\) ∽ \(\Delta A'B'H'\) (c-g-c)
=> \(\widehat A = \widehat {A'}\) (cặp góc tương ứng)
Trang 56 và 57 SGK Toán 8 thường chứa các bài tập liên quan đến các kiến thức đã học trong chương. Các dạng bài tập thường gặp bao gồm:
Để giải quyết các bài tập trên trang 56, học sinh cần nắm vững các kiến thức về:
Ví dụ, bài tập 1 trang 56 có thể yêu cầu chứng minh một tứ giác là hình bình hành. Để làm được điều này, học sinh cần áp dụng các dấu hiệu nhận biết hình bình hành, chẳng hạn như:
Trang 57 thường tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Các bài tập có thể yêu cầu:
Ví dụ, bài tập 3 trang 57 có thể yêu cầu tính diện tích của một hình thang. Để làm được điều này, học sinh cần sử dụng công thức tính diện tích hình thang: S = (a + b)h/2, trong đó a và b là độ dài hai đáy, h là chiều cao.
Để giải bài tập Toán 8 trang 56, 57 một cách hiệu quả, học sinh nên:
Khi giải bài tập Toán 8, học sinh cần chú ý:
Giaitoan.edu.vn không chỉ cung cấp lời giải chi tiết cho các bài tập trong SGK mà còn cung cấp nhiều tài liệu học tập hữu ích khác, như:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá và tận hưởng những lợi ích tuyệt vời mà chúng tôi mang lại!
| Công thức | Mô tả |
|---|---|
| Diện tích hình thang | S = (a + b)h/2 |
| Định lý Pitago | a2 + b2 = c2 |