Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 4.3 trang 95 SGK Toán 8 một cách nhanh chóng và hiệu quả.
Chúng tôi không chỉ cung cấp đáp án mà còn giải thích rõ ràng từng bước giải, giúp bạn hiểu sâu sắc kiến thức và rèn luyện kỹ năng giải toán.
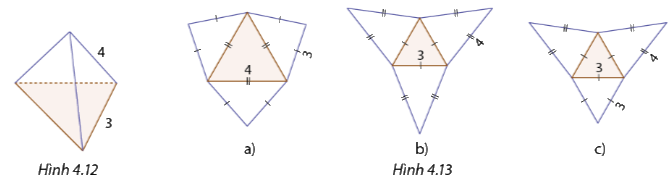
Cho hình chóp tam giác đều có độ dài cạnh bên bằng
Đề bài
Cho hình chóp tam giác đều có độ dài cạnh bên bằng \(4\,cm\) và độ dài cạnh đáy bằng \(3\,cm\) như Hình 4.12. Trong hình 4.13, hình nào là hình khai triển của hình chóp tam giác đều đã cho?
Phương pháp giải - Xem chi tiết
Dựa vào dấu hiệu nhận biết của hình chóp tam giác đều và hình chóp tứ giác đều để xác định.
Lời giải chi tiết
Hình b) là hình khai triển của hình chóp tam giác đều đã cho vì nó có các cạnh bên bằng nhau bằng 4 và đáy là tam giác đều cạnh bằng 3.
Bài 4.3 trang 95 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh chứng minh một tính chất hoặc giải một bài toán liên quan đến hình chữ nhật.
Bài tập 4.3 thường có dạng như sau: Cho hình chữ nhật ABCD, trên cạnh BC lấy điểm E. Gọi I là giao điểm của AE và BD. Chứng minh rằng: (a) IA = IB; (b) DI = 2AI.
Để giải bài tập này, chúng ta cần vận dụng các kiến thức sau:
(a) Chứng minh IA = IB:
(b) Chứng minh DI = 2AI:
Khi giải bài tập này, bạn cần chú ý:
Để củng cố kiến thức về hình chữ nhật và các bài toán liên quan, bạn có thể làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tìm hiểu thêm về các loại hình bình hành khác như hình thoi, hình bình hành và các tính chất của chúng.
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài 4.3 trang 95 SGK Toán 8 và tự tin giải các bài tập tương tự. Chúc bạn học tốt!