Giải bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều

Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho bài tập 1 trang 108 sách giáo khoa Toán 9 tập 2, chương trình Cánh diều.

Chúng tôi hiểu rằng việc tự học và làm bài tập đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

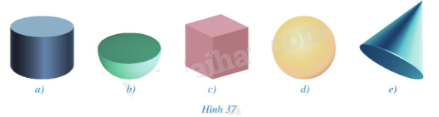
Trong những vật thể ở các hình 37a, 37b, 37c, 37d, 37e, vật thể ở hình nào có dạng hình cầu?

Đề bài

Trong những vật thể ở các hình 37a, 37b, 37c, 37d, 37e, vật thể ở hình nào có dạng hình cầu?

Giải bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều 2

Hình được tạo ra khi quay một nửa đường tròn một vòng quanh đường thẳng cố định chứa đường kính là một hình cầu.

Lời giải chi tiết

Vật thể ở hình 37d có dạng hình cầu.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều đặc sắc thuộc chuyên mục bài tập toán 9 trên nền tảng học toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều: Tổng quan

Bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số, tập xác định, tập giá trị, và cách xác định hàm số bằng công thức để giải quyết các bài toán cụ thể.

Nội dung bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều

Bài tập 1 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:

Xác định hàm số bậc hai trong các hàm số đã cho.
Tìm tập xác định của hàm số bậc hai.
Xác định hệ số a, b, c của hàm số bậc hai.
Tìm điểm thuộc đồ thị hàm số.

Phương pháp giải bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều

Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:

Định nghĩa hàm số bậc hai: Hàm số bậc hai có dạng y = ax² + bx + c, trong đó a, b, c là các số thực và a ≠ 0.
Tập xác định: Tập xác định của hàm số bậc hai là tập hợp tất cả các giá trị của x mà tại đó hàm số có nghĩa. Trong trường hợp hàm số bậc hai, tập xác định là tập R (tập hợp tất cả các số thực).
Hệ số a, b, c: Trong hàm số y = ax² + bx + c, a là hệ số của x², b là hệ số của x, và c là hệ số tự do.
Điểm thuộc đồ thị hàm số: Một điểm (x₀; y₀) thuộc đồ thị hàm số y = f(x) nếu y₀ = f(x₀).

Lời giải chi tiết bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều

Câu a: Hàm số y = 2x² + 5x - 3 là hàm số bậc hai vì nó có dạng y = ax² + bx + c với a = 2, b = 5, và c = -3. Tập xác định của hàm số là R.

Câu b: Hàm số y = -x + 1 không phải là hàm số bậc hai vì nó không có dạng y = ax² + bx + c. Đây là hàm số bậc nhất.

Câu c: Hàm số y = x² - 4x là hàm số bậc hai vì nó có dạng y = ax² + bx + c với a = 1, b = -4, và c = 0. Tập xác định của hàm số là R.

Ví dụ minh họa

Xét hàm số y = x² - 2x + 1. Để xác định xem điểm A(0; 1) có thuộc đồ thị hàm số hay không, ta thay x = 0 vào hàm số:

y = (0)² - 2(0) + 1 = 1

Vì y = 1, nên điểm A(0; 1) thuộc đồ thị hàm số y = x² - 2x + 1.

Bài tập luyện tập

Để củng cố kiến thức, các em có thể tự giải các bài tập sau:

Xác định hàm số bậc hai trong các hàm số sau: y = 3x² - x + 2, y = -2x + 5, y = x² + 1.
Tìm tập xác định của các hàm số sau: y = 4x² - 7x + 1, y = -x² + 3.

Kết luận

Bài tập 1 trang 108 SGK Toán 9 tập 2 - Cánh diều là một bài tập cơ bản giúp học sinh làm quen với các khái niệm về hàm số bậc hai. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ là nền tảng vững chắc cho các bài học tiếp theo. Chúc các em học tập tốt!