Chào mừng bạn đến với bài học lý thuyết Bất đẳng thức Toán 9 Cánh diều tại giaitoan.edu.vn! Bất đẳng thức là một phần quan trọng trong chương trình Toán 9, giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề.
Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về lý thuyết bất đẳng thức, bao gồm các định nghĩa, tính chất và ứng dụng quan trọng. Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa để bạn có thể nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
1. Nhắc lại thứ tự trong tập hợp số thực Trong hai số khác nhau luôn có số này nhỏ hơn số kia.
1. Nhắc lại thứ tự trong tập hợp số thực
Trong hai số khác nhau luôn có số này nhỏ hơn số kia.
- Nếu số thực a nhỏ hơn số thực b thì ta viết \(a < b\) hay \(b > a\).
- Số thực lớn hơn 0 gọi là số thực dương.
- Số thực nhỏ hơn 0 gọi là số thực âm.
Ta có các kết quả:
- Trên trục số nằm ngang, nếu số thực a nằm bên trái số thực b thì \(a < b\) hay \(b > a\).

- Tổng của hai số thực dương là số thực dương. Tổng của hai số thực âm là số thực âm.
- Với hai số thực a, b, ta có:
\(ab > 0\) thì a, b cùng dương hoặc cùng âm (hay a, b cùng dấu) và ngược lại:
\(ab < 0\) thì a, b trái dấu và ngược lại.
- Với a, b là hai số thực dương, nếu \(a > b\) thì \(\sqrt a > \sqrt b \).
2. Bất đẳng thức
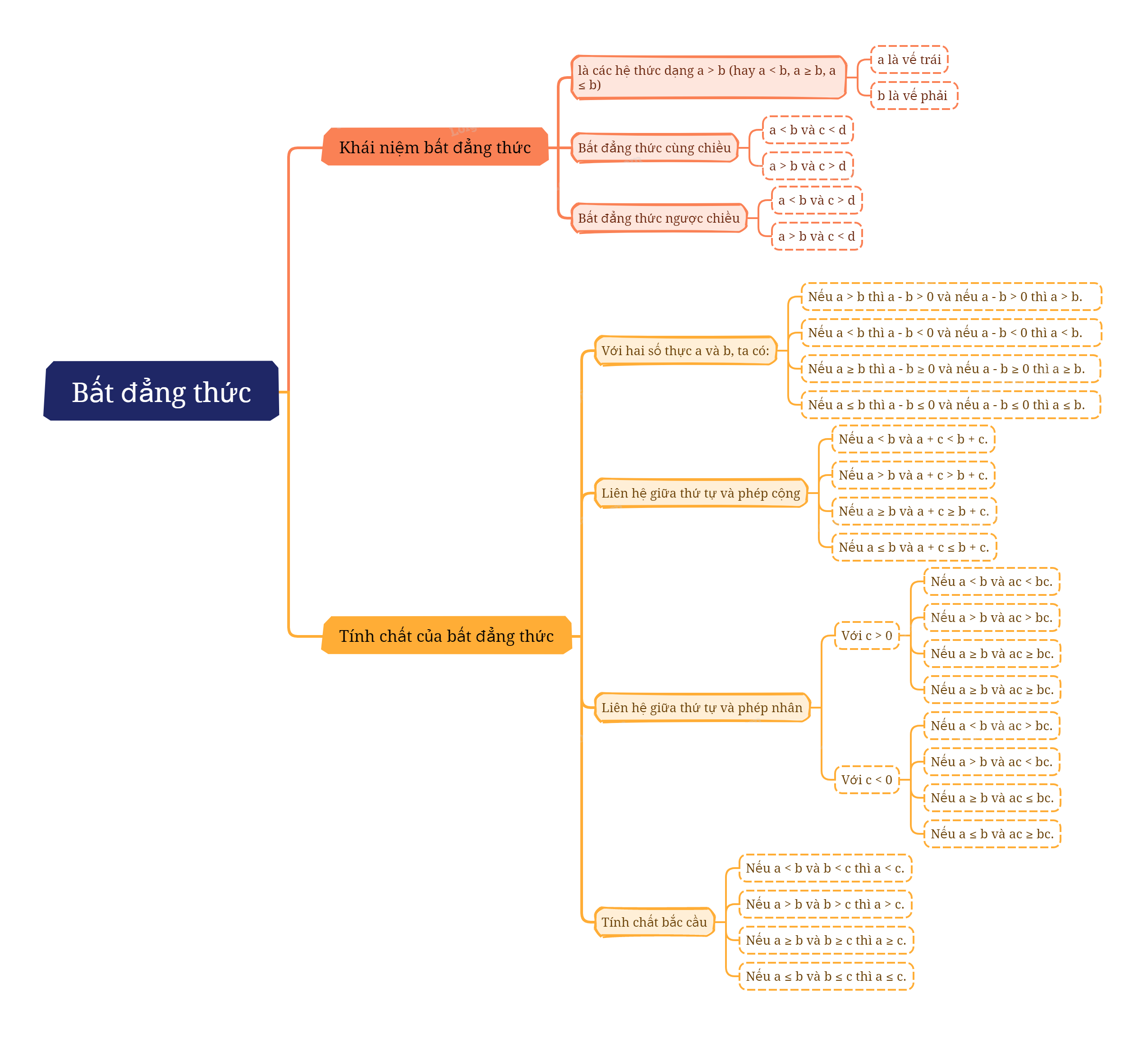
Khái niệm bất đẳng thức
Ta gọi hệ thức dạng \(a > b\) (hay \(a < b\), \(a \ge b\), \(a \le b\)) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức. |
Chú ý:
Hai bất đẳng thức \(a < b\) và \(c < d\) (hay \(a > b\) và \(c > d\)) được gọi là hai bất đẳng thức cùng chiều.
Hai bất đẳng thức \(a < b\) và \(c > d\) (hay \(a > b\) và \(c < d\)) được gọi là hai bất đẳng thức ngược chiều.
Tính chất của bất đẳng thức
Với hai số thực a và b, ta có: - Nếu \(a > b\) thì \(a - b > 0\). Ngược lại, nếu \(a - b > 0\) thì \(a > b\). - Nếu \(a < b\) thì \(a - b < 0\). Ngược lại, nếu \(a - b < 0\) thì \(a < b\). - Nếu \(a \ge b\) thì \(a - b \ge 0\). Ngược lại, nếu \(a - b \ge 0\) thì \(a \ge b\). - Nếu \(a \le b\) thì \(a - b \le 0\). Ngược lại, nếu \(a - b \le 0\) thì \(a \le b\). |
Nhận xét: Do khẳng định nêu trên, để chứng minh \(a > b\), ta có thể chứng minh \(a - b > 0\) hoặc chứng minh \(b - a < 0\).
Liên hệ giữa thứ tự và phép cộng
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Nếu \(a < b\) thì \(a + c < b + c\). Nếu \(a > b\) thì \(a + c > b + c\). Nếu \(a \le b\) thì \(a + c \le b + c\). Nếu \(a \ge b\) thì \(a + c \ge b + c\). |
Ví dụ:Vì \(2023 < 2024\) nên \(2023 + \left( { - 19} \right) < 2024 + \left( { - 19} \right)\)
Liên hệ giữa thứ tự và phép nhân
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương, ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Với ba số a, b, c mà c > 0, ta có: - Nếu \(a < b\) thì \(ac < bc\). - Nếu \(a > b\) thì \(ac > bc\). - Nếu \(a \le b\) thì \(ac \le bc\). - Nếu \(a \ge b\) thì \(ac \ge bc\). |
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
Với ba số a, b, c và c < 0, ta có: Nếu \(a < b\) thì \(ac > bc\). Nếu \(a > b\) thì \(ac < bc\). Nếu \(a \le b\) thì \(ac \ge bc\). Nếu \(a \ge b\) thì \(ac \le bc\). |
Ví dụ:
Vì \( - 7 < - 5\) và \(3 > 0\) nên \(3.\left( { - 7} \right) < 3.\left( { - 5} \right)\).
Vì \( - 7 < - 5\) và \( - 3 < 0\) nên \(\left( { - 3} \right).\left( { - 7} \right) > \left( { - 3} \right).\left( { - 5} \right)\).
Tính chất bắc cầu của bất đẳng thức
Nếu \(a > b\) và \(b > c\) thì \(a > c\). |
Ví dụ: Vì \(\frac{{2024}}{{2023}} = 1 + \frac{1}{{2023}} > 1\) và \(\frac{{2021}}{{2022}} = 1 - \frac{1}{{2022}} < 1\) nên \(\frac{{2024}}{{2023}} > \frac{{2021}}{{2022}}\).
Bất đẳng thức là một biểu thức toán học so sánh hai giá trị, sử dụng các ký hiệu >, <, ≥, ≤, ≠. Trong chương trình Toán 9, học sinh sẽ được làm quen với các loại bất đẳng thức cơ bản và các phương pháp giải bất đẳng thức.
Để giải bất đẳng thức, chúng ta cần sử dụng các quy tắc biến đổi bất đẳng thức một cách hợp lý:
Bất đẳng thức có nhiều ứng dụng trong thực tế, ví dụ:
Ví dụ 1: Giải bất đẳng thức 2x + 3 > 5
Giải:
Vậy tập nghiệm của bất đẳng thức là x > 1.
Ví dụ 2: Chứng minh bất đẳng thức a2 + b2 ≥ 2ab với mọi số thực a và b.
Giải:
Ta có: (a - b)2 ≥ 0 với mọi số thực a và b.
Khai triển biểu thức, ta được: a2 - 2ab + b2 ≥ 0
Suy ra: a2 + b2 ≥ 2ab (đpcm)
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết Bất đẳng thức Toán 9 Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài toán liên quan.