Chào mừng các em học sinh đến với lời giải chi tiết bài tập 5 trang 110 SGK Toán 9 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 5 thuộc chương trình học Toán 9 tập 2, tập trung vào việc vận dụng các kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Chúng tôi sẽ hướng dẫn các em từng bước để hiểu rõ cách tiếp cận và giải quyết bài toán này.
Phần đựng được nước của một chiếc ly có dạng hình nón với bán kính đáy là R và chiều cao là H (Hình 43a). Người ta đổ nước vào ly đó sao cho chiều cao của khối nước đó bằng (frac{H}{2}) và bán kính đáy của khối nước đó bằng (frac{R}{2}) Tính theo R và H thể tích phần không chứa nước của chiếc ly ở Hình 43b.
Đề bài
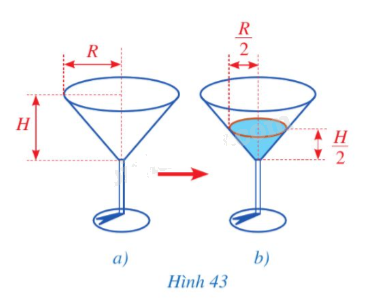
Phần đựng được nước của một chiếc ly có dạng hình nón với bán kính đáy là R và chiều cao là H (Hình 43a). Người ta đổ nước vào ly đó sao cho chiều cao của khối nước đó bằng \(\frac{H}{2}\) và bán kính đáy của khối nước đó bằng \(\frac{R}{2}\) Tính theo R và H thể tích phần không chứa nước của chiếc ly ở Hình 43b.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Bước 1: Tính thể tích chiếc ly.
Bước 2: Tính thể tích phần nước.
Bước 3: Thể tích phần không chứa nước = thể tích chiếc ly - thể tích phần nước.
Lời giải chi tiết
Thể tích chiếc ly là:
\(\frac{1}{3}\pi {R^2}H\) (đvtt).
Thể tích phần nước đổ vào là:
\(\frac{1}{3}\pi {\left( {\frac{R}{2}} \right)^2}\frac{H}{2} = \frac{{\pi {R^2}H}}{{24}}\) (đvtt).
Thể tích phần không chứa nước là:
\(\frac{1}{3}\pi {R^2}H - \frac{{\pi {R^2}H}}{{24}} = \frac{{7\pi {R^2}H}}{{24}}\) (đvtt).
Bài tập 5 trang 110 SGK Toán 9 tập 2 - Cánh diều yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết một bài toán thực tế liên quan đến quỹ đạo của một vật được ném lên. Để giải bài tập này, chúng ta cần xác định được hàm số bậc hai mô tả quỹ đạo của vật và sau đó tìm các giá trị cần thiết.
Đề bài thường cung cấp các thông tin về vị trí ban đầu của vật, vận tốc ban đầu và góc ném. Dựa vào các thông tin này, chúng ta có thể xây dựng hệ tọa độ và xác định phương trình quỹ đạo của vật. Phương trình này thường có dạng y = ax2 + bx + c, trong đó a, b, c là các hệ số cần xác định.
Để tìm các hệ số a, b, c, chúng ta cần sử dụng các thông tin đã cho trong đề bài. Ví dụ, nếu chúng ta biết vị trí ban đầu của vật là (x0, y0), thì ta có thể thay x = x0 và y = y0 vào phương trình y = ax2 + bx + c để được một phương trình liên quan đến a, b, c. Tương tự, chúng ta có thể sử dụng thông tin về vận tốc ban đầu để tìm thêm các phương trình khác.
Sau khi có đủ các phương trình liên quan đến a, b, c, chúng ta có thể giải hệ phương trình này để tìm ra giá trị của a, b, c. Có nhiều phương pháp để giải hệ phương trình, chẳng hạn như phương pháp thế, phương pháp cộng đại số hoặc sử dụng máy tính bỏ túi.
Sau khi đã tìm được các hệ số a, b, c, chúng ta có thể sử dụng hàm số y = ax2 + bx + c để giải quyết các câu hỏi của bài toán. Ví dụ, chúng ta có thể tìm khoảng cách lớn nhất mà vật đạt được, thời gian vật bay trong không khí hoặc vị trí của vật tại một thời điểm nhất định.
Giả sử đề bài cho biết một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 20 m/s và góc ném là 30 độ so với phương ngang. Hãy tìm phương trình quỹ đạo của quả bóng và khoảng cách lớn nhất mà quả bóng đạt được.
Bài tập 5 trang 110 SGK Toán 9 tập 2 - Cánh diều là một bài tập điển hình về ứng dụng của hàm số bậc hai trong thực tế. Việc nắm vững kiến thức về hàm số và phương pháp giải bài tập sẽ giúp các em tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.
Hy vọng với hướng dẫn chi tiết này, các em sẽ hiểu rõ cách giải bài tập 5 trang 110 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!