Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho bài tập 1 trang 122 SGK Toán 9 tập 1, thuộc chương trình Toán 9 Cánh diều.
Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Quan sát các hình 83, 84, 85, 86. a) Tính diện tích phần được tô màu trong mỗi hình đó. b) Tính độ dài cung tròn được tô màu xanh ở mỗi hình 83, 84.
Đề bài
Quan sát các hình 83, 84, 85, 86.
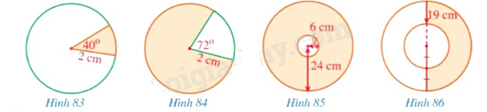
a) Tính diện tích phần được tô màu trong mỗi hình đó.
b) Tính độ dài cung tròn được tô màu xanh ở mỗi hình 83, 84.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào các kiến thức đã học để tính.
Lời giải chi tiết
a)
+ Hình 83: Diện tích hình quạt tròn đó là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.2}^2}.40}}{{360}} = \frac{{4\pi }}{9}\left( {c{m^2}} \right)\)
+ Hình 84: Diện tích hình quạt tròn đó là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.2}^2}.\left( {360 - 72} \right)}}{{360}} = \frac{{4\pi .288}}{{360}} = \frac{{16\pi }}{5}\left( {c{m^2}} \right)\)
+ Hình 85: Diện tích hình vành khuyên đó là:
\(S = \pi \left( {{R^2} - {r^2}} \right) = \pi \left( {{{24}^2} - {6^2}} \right) = 540\pi \left( {c{m^2}} \right)\)
+ Hình 86: Diện tích hình vành khuyên đó là:
\(S = \frac{1}{2}\pi \left( {{R^2} - {r^2}} \right) = \frac{1}{2}\pi \left[ {{{\left( {2.19} \right)}^2} - {{19}^2}} \right] = \frac{1083}{2}\pi \left( {c{m^2}} \right)\)
b)
+ Hình 83: Độ dài cung tròn tô màu xanh là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.\left( {360 - 40} \right)}}{{180}} = \frac{{2\pi .320}}{{180}} = \frac{{32\pi }}{9}\left( {cm} \right)\)
+ Hình 84: Độ dài cung tròn tô màu xanh là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.72}}{{180}} = \frac{{4\pi }}{5}\left( {cm} \right)\)
Bài tập 1 trang 122 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và đường thẳng song song, vuông góc.
Bài tập 1 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đường thẳng có phương trình y = -2x + 3. Hệ số góc của đường thẳng này là a = -2.
Đường thẳng song song với đường thẳng y = -2x + 3 có cùng hệ số góc là -2. Vậy phương trình đường thẳng song song có dạng y = -2x + c (c ≠ 3).
Đường thẳng vuông góc với đường thẳng y = -2x + 3 có hệ số góc là m sao cho (-2) * m = -1. Suy ra m = 1/2. Vậy phương trình đường thẳng vuông góc có dạng y = (1/2)x + c.
Đường thẳng đi qua điểm A(1; 2) và song song với đường thẳng y = -2x + 3 có hệ số góc là -2. Phương trình đường thẳng có dạng y = -2x + b. Thay tọa độ điểm A(1; 2) vào phương trình, ta có: 2 = -2 * 1 + b. Suy ra b = 4. Vậy phương trình đường thẳng cần tìm là y = -2x + 4.
Cho đường thẳng y = 3x - 1. Hãy tìm phương trình đường thẳng:
Giải:
Hãy tự giải các bài tập sau để củng cố kiến thức:
Bài tập 1 trang 122 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các tính chất của nó. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn khi giải các bài tập tương tự.