Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 36, 37, 38 sách giáo khoa Toán 9 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hình 25 mô tả một đĩa tròn bằng bìa cứng được chia làm 12 phần bằng nhau và ghi các số 1,2,3,…,12; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Xét phép thử ‘Quay đĩa tròn một lần”. a) Viết tập hợp Ω gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại. b) Liệt kê các kết quả thuận lợi cho biến cố A: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 3”. c) Tìm tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của tập hợp Ω.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 38 SGK Toán 9 Cánh diều
Nền ẩm thực Việt Nam được đánh giá cao trên thế giới, thu hút nhiều người sành ăn trong nước và quốc tế. 16 món ngon đặc sắc đến từ các tỉnh, thành phố được chọn ra như sau: phở Thìn (Hà Nội), bánh đa kế (Bắc Ninh), bánh đậu xanh (Hải Dương), bún cá cay (Hải Phòng), gà đồi Yên Thế (Bắc Giang), nộm da trâu (Sơn la), thắng cố (Lào Cai), miến lươn (Nghệ An), cơm hến (Huế), cá mực nhảy (Hà Tĩnh), bánh mì Hội An (Quảng Nam), sủi cảo (TP Hồ Chí Minh), bánh canh Trảng Bàng (Tây Ninh), cá lóc nướng (Cần Thơ), cơm dừa (Bến Tre), gỏi cá (Kiên Giang).
Chọn ngẫu nhiên một món trong 16 món ngon đó. Tính xác suất của mỗi biến cố sau:
a) S: “Món ngon được chọn thuộc miền Bắc”
b) T: “Món ngon được chọn thuộc miền Trung”.
c) U: “Món ngon được chọn thuộc miền Nam”.
Phương pháp giải:
Bước 1: Đếm số kết quả có thể xảy ra.
Bước 2: Đếm số kết quả thận lợi cho từng biến cố.
Bước 3: Lập tỉ số giữa số liệu ở bước 1 và bước 2.
Lời giải chi tiết:
Xét phép thử "Chọn ngẫu nhiên 1 trong 16 món”.
Ta thấy, các kết quả có thể xảy ra của phép thử đó là đồng khả năng.
Có 16 khả năng có thể xảy ra khi chọn ngẫu nhiên 1 trong 16 món.
a) Có 7 kết quả thuận lợi cho biến cố S: “Món ngon được chọn thuộc miền Bắc” là: phở Thìn (Hà Nội), bánh đa kế (Bắc Ninh), bánh đậu xanh (Hải Dương), bún cá cay (Hải Phòng), gà đồi Yên Thế (Bắc Giang), nộm da trâu (Sơn la), thắng cố (Lào Cai),
Vậy \(P(S) = \frac{7}{{16}}\)
b) Có 4 kết quả thuận lợi cho biến cố T: “Món ngon được chọn thuộc miền Trung” là: miến lươn (Nghệ An), cơm hến (Huế), cá mực nhảy (Hà Tĩnh), bánh mì Hội An (Quảng Nam)
Vậy \(P(T) = \frac{4}{{16}} = \frac{1}{4}\)
c) Có 5 kết quả thuận lợi cho biến cố U: “Món ngon được chọn thuộc miền Nam” là: sủi cảo (TP Hồ Chí Minh), bánh canh Trảng Bàng (Tây Ninh), cá lóc nướng (Cần Thơ), cơm dừa (Bến Tre), gỏi cá (Kiên Giang).
Vậy \(P(U) = \frac{5}{{16}}\)
Video hướng dẫn giải
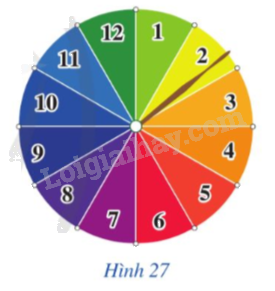
Trả lời câu hỏi Luyện tập 2 trang 37 SGK Toán 9 Cánh diều
Trong Hoạt động 2, tính xác suất của biến cố D: “Chiếc kim chỉ vào hình quạt ghi số nguyên tố”.
Phương pháp giải:
Bước 1: Kiểm tra tính đồng khả năng đối với các kết quả có thể xảy ra.
Bước 2: Đếm số kết quả có thể xảy ra, tức là đếm số phần tử của không gian mẫu Ω.
Bước 3: Đếm số kết quả thuận lợi cho biến cố A.
Bước 4: Lập tỉ số giữa kết quả thuận lợi cho biến cố A và tổng số kết quả có thể xảy ra.
Lời giải chi tiết:
Xét phép thử "Quay đĩa tròn một lần”.
Ta thấy, các kết quả có thể xảy ra của phép thử đó là đồng khả năng.
Có 12 khả năng có thể xảy ra của kim chỉ vào hình quạt khi quay đĩa tròn 1 lần: số 1, số 2, số 3, số 4, …, số 12.
Có 6 kết quả thuận lợi cho biến cố D: “Chiếc kim chỉ vào hình quạt ghi số nguyên tố” là: số 2, số 3, số 5, số 7, số 11.
Vậy \(P(D) = \frac{5}{{12}}\)
Video hướng dẫn giải
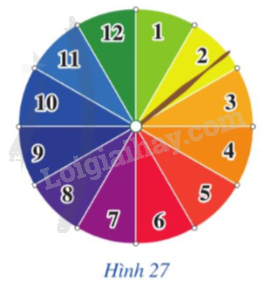
Trả lời câu hỏi Hoạt động 2 trang 36 SGK Toán 9 Cánh diều
Hình 27 mô tả một đĩa tròn bằng bìa cứng được chia làm 12 phần bằng nhau và ghi các số 1,2,3,…,12; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.
Xét phép thử "Quay đĩa tròn một lần”.
a) Viết tập hợp Ω gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.
b) Liệt kê các kết quả thuận lợi cho biến cố A: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 3”.
c) Tìm tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của tập hợp Ω.
Phương pháp giải:
a) Chỉ ra các khả năng có thể xảy ra khi đĩa dừng lại.
b) Tìm các số ghi trên quạt chia hết cho 3.
c) Tỉ số:

Lời giải chi tiết:
a) Ω = {số 1; số 2; số 3; số 4;….., số 11, số 12}.
b) Các kết quả thuận lợi cho biến cố A: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 3” là số 3, số 6, số 9, số 12 (có 4 kết quả)
c) Tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của tập hợp Ω là:
\(\frac{4}{{12}} = \frac{1}{3}\)
Video hướng dẫn giải
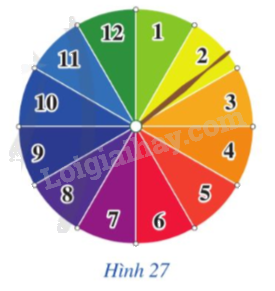
Trả lời câu hỏi Hoạt động 2 trang 36 SGK Toán 9 Cánh diều
Hình 27 mô tả một đĩa tròn bằng bìa cứng được chia làm 12 phần bằng nhau và ghi các số 1,2,3,…,12; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.
Xét phép thử "Quay đĩa tròn một lần”.
a) Viết tập hợp Ω gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.
b) Liệt kê các kết quả thuận lợi cho biến cố A: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 3”.
c) Tìm tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của tập hợp Ω.
Phương pháp giải:
a) Chỉ ra các khả năng có thể xảy ra khi đĩa dừng lại.
b) Tìm các số ghi trên quạt chia hết cho 3.
c) Tỉ số:

Lời giải chi tiết:
a) Ω = {số 1; số 2; số 3; số 4;….., số 11, số 12}.
b) Các kết quả thuận lợi cho biến cố A: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 3” là số 3, số 6, số 9, số 12 (có 4 kết quả)
c) Tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của tập hợp Ω là:
\(\frac{4}{{12}} = \frac{1}{3}\)
Video hướng dẫn giải
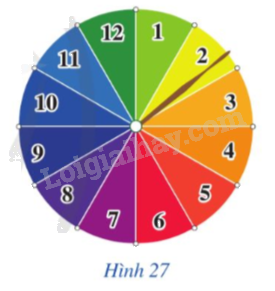
Trả lời câu hỏi Luyện tập 2 trang 37 SGK Toán 9 Cánh diều
Trong Hoạt động 2, tính xác suất của biến cố D: “Chiếc kim chỉ vào hình quạt ghi số nguyên tố”.
Phương pháp giải:
Bước 1: Kiểm tra tính đồng khả năng đối với các kết quả có thể xảy ra.
Bước 2: Đếm số kết quả có thể xảy ra, tức là đếm số phần tử của không gian mẫu Ω.
Bước 3: Đếm số kết quả thuận lợi cho biến cố A.
Bước 4: Lập tỉ số giữa kết quả thuận lợi cho biến cố A và tổng số kết quả có thể xảy ra.
Lời giải chi tiết:
Xét phép thử "Quay đĩa tròn một lần”.
Ta thấy, các kết quả có thể xảy ra của phép thử đó là đồng khả năng.
Có 12 khả năng có thể xảy ra của kim chỉ vào hình quạt khi quay đĩa tròn 1 lần: số 1, số 2, số 3, số 4, …, số 12.
Có 6 kết quả thuận lợi cho biến cố D: “Chiếc kim chỉ vào hình quạt ghi số nguyên tố” là: số 2, số 3, số 5, số 7, số 11.
Vậy \(P(D) = \frac{5}{{12}}\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 38 SGK Toán 9 Cánh diều
Nền ẩm thực Việt Nam được đánh giá cao trên thế giới, thu hút nhiều người sành ăn trong nước và quốc tế. 16 món ngon đặc sắc đến từ các tỉnh, thành phố được chọn ra như sau: phở Thìn (Hà Nội), bánh đa kế (Bắc Ninh), bánh đậu xanh (Hải Dương), bún cá cay (Hải Phòng), gà đồi Yên Thế (Bắc Giang), nộm da trâu (Sơn la), thắng cố (Lào Cai), miến lươn (Nghệ An), cơm hến (Huế), cá mực nhảy (Hà Tĩnh), bánh mì Hội An (Quảng Nam), sủi cảo (TP Hồ Chí Minh), bánh canh Trảng Bàng (Tây Ninh), cá lóc nướng (Cần Thơ), cơm dừa (Bến Tre), gỏi cá (Kiên Giang).
Chọn ngẫu nhiên một món trong 16 món ngon đó. Tính xác suất của mỗi biến cố sau:
a) S: “Món ngon được chọn thuộc miền Bắc”
b) T: “Món ngon được chọn thuộc miền Trung”.
c) U: “Món ngon được chọn thuộc miền Nam”.
Phương pháp giải:
Bước 1: Đếm số kết quả có thể xảy ra.
Bước 2: Đếm số kết quả thận lợi cho từng biến cố.
Bước 3: Lập tỉ số giữa số liệu ở bước 1 và bước 2.
Lời giải chi tiết:
Xét phép thử "Chọn ngẫu nhiên 1 trong 16 món”.
Ta thấy, các kết quả có thể xảy ra của phép thử đó là đồng khả năng.
Có 16 khả năng có thể xảy ra khi chọn ngẫu nhiên 1 trong 16 món.
a) Có 7 kết quả thuận lợi cho biến cố S: “Món ngon được chọn thuộc miền Bắc” là: phở Thìn (Hà Nội), bánh đa kế (Bắc Ninh), bánh đậu xanh (Hải Dương), bún cá cay (Hải Phòng), gà đồi Yên Thế (Bắc Giang), nộm da trâu (Sơn la), thắng cố (Lào Cai),
Vậy \(P(S) = \frac{7}{{16}}\)
b) Có 4 kết quả thuận lợi cho biến cố T: “Món ngon được chọn thuộc miền Trung” là: miến lươn (Nghệ An), cơm hến (Huế), cá mực nhảy (Hà Tĩnh), bánh mì Hội An (Quảng Nam)
Vậy \(P(T) = \frac{4}{{16}} = \frac{1}{4}\)
c) Có 5 kết quả thuận lợi cho biến cố U: “Món ngon được chọn thuộc miền Nam” là: sủi cảo (TP Hồ Chí Minh), bánh canh Trảng Bàng (Tây Ninh), cá lóc nướng (Cần Thơ), cơm dừa (Bến Tre), gỏi cá (Kiên Giang).
Vậy \(P(U) = \frac{5}{{16}}\)
Mục 2 của chương trình Toán 9 tập 2 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định các yếu tố của hàm số bậc hai (hệ số a, b, c), tìm đỉnh của parabol, vẽ đồ thị hàm số và xét tính đơn điệu của hàm số. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc hai, các công thức tính đỉnh của parabol và các tính chất của đồ thị hàm số.
Bài tập này yêu cầu học sinh giải các phương trình bậc hai một ẩn bằng các phương pháp khác nhau (phân tích thành nhân tử, sử dụng công thức nghiệm, sử dụng định lý Vi-et). Để giải bài tập này, học sinh cần nắm vững các phương pháp giải phương trình bậc hai và các định lý liên quan.
Bài tập này yêu cầu học sinh vận dụng kiến thức về phương trình bậc hai để giải các bài toán thực tế (ví dụ: tính chiều dài, chiều rộng của một hình chữ nhật, tính vận tốc, thời gian của một vật chuyển động). Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các đại lượng cần tìm và lập phương trình bậc hai tương ứng.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 2 trang 36, 37, 38 SGK Toán 9 tập 2 - Cánh diều:
Khi giải bài tập trong mục 2, học sinh cần lưu ý những điều sau:
Để học tốt môn Toán 9, học sinh có thể tham khảo các tài liệu sau:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 2 trang 36, 37, 38 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!