Phép quay là một trong những phép biến hình quan trọng trong chương trình Toán 9, đặc biệt là sách Cánh diều. Việc nắm vững lý thuyết về phép quay không chỉ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả mà còn là bước đệm quan trọng cho các kiến thức nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về lý thuyết Phép quay Toán 9 Cánh diều, giúp học sinh tự tin chinh phục môn Toán.
1. Khái niệm - Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a).
1. Khái niệm
- Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
|
Phép quay giữ nguyên hình đa giác đều
- Cho hình đa giác đều \({A_1}{A_2} \ldots {A_n}(n \ge 3,n \in {\rm{N}})\) có tâm \(O\). Phép quay giữ nguyên hình đa giác đều \({A_1}{A_2} \ldots {A_n}\) là phép quay tâm \(O\) biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đểu đó. - Người ta chứng minh được rằng chỉ có các phép quay sau đây giữ nguyên hình đa giác đều \({A_1}{A_2} \ldots {A_n}(n \ge 3,n \in {\rm{N}})\) với tâm \(O\): các phép quay thuận chiểu \(\alpha ^\circ \) tâm \(O\) và các phép quay ngược chiểu \(\alpha ^\circ \) tâm \(O\), với \(\alpha ^\circ \) lần lượt nhận các giá trị \(\alpha _1^{\rm{o}} = \frac{{360^\circ }}{n};\alpha _2^{\rm{o}} = \frac{{2 \cdot 360^\circ }}{n}; \ldots ;\alpha _n^{\rm{o}} = \frac{{n \cdot 360^\circ }}{n} = 360^\circ \) |
Ví dụ:
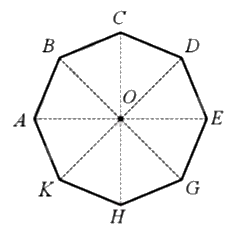
Phép quay thuận chiều \(45^\circ \) tâm O biến điểm A thành điểm B thì phép quay đó biến các điểm C, D, H, K tương ứng thành các điểm D, E, K, A.

Phép quay là một phép biến hình trong mặt phẳng, biến mỗi điểm M thành một điểm M' sao cho khoảng cách từ M đến tâm quay O bằng khoảng cách từ M' đến tâm quay O, và góc quay (OM, OM') là một góc định trước.
1. Định nghĩa:
Phép quay tâm O với góc α (α đo theo độ, chiều dương là chiều ngược chiều kim đồng hồ) là phép biến hình biến mỗi điểm M thành điểm M' sao cho:
Ký hiệu: QO(α)(M) = M'
2. Tính chất của phép quay:
3. Phép quay và tam giác:
Phép quay biến một tam giác thành một tam giác bằng nó.
4. Biểu thức tọa độ của phép quay:
Trong mặt phẳng tọa độ Oxy, cho điểm M(x; y) và phép quay QO(α) với tâm O(0; 0). Tọa độ điểm M'(x'; y') sau phép quay được tính theo công thức:
x' = x.cos(α) - y.sin(α)
y' = x.sin(α) + y.cos(α)
Nếu tâm quay O(a; b) thì công thức tọa độ sẽ là:
x' = (x - a).cos(α) - (y - b).sin(α) + a
y' = (x - a).sin(α) + (y - b).cos(α) + b
Dạng 1: Xác định ảnh của một điểm qua phép quay
Để giải loại bài này, học sinh cần nắm vững công thức tọa độ của phép quay và áp dụng chính xác.
Dạng 2: Chứng minh hai hình bằng nhau qua phép quay
Sử dụng tính chất bảo toàn khoảng cách và góc của phép quay để chứng minh hai tam giác hoặc hai đa giác bằng nhau.
Dạng 3: Ứng dụng phép quay vào giải quyết các bài toán hình học
Ví dụ: Tìm ảnh của một đường thẳng, một đường tròn qua phép quay.
Cho điểm A(2; 1) và phép quay QO(90°) với tâm O(0; 0). Tìm tọa độ điểm A' là ảnh của A qua phép quay.
Giải:
x' = 2.cos(90°) - 1.sin(90°) = 2.0 - 1.1 = -1
y' = 2.sin(90°) + 1.cos(90°) = 2.1 + 1.0 = 2
Vậy A'(-1; 2)
Để nắm vững lý thuyết và kỹ năng giải bài tập về phép quay, học sinh nên luyện tập thường xuyên với các bài tập đa dạng. Giaitoan.edu.vn cung cấp hệ thống bài tập phong phú, được phân loại theo mức độ khó, giúp học sinh tự đánh giá và cải thiện khả năng của mình.
Lý thuyết Phép quay Toán 9 Cánh diều là một phần quan trọng của chương trình học. Việc hiểu rõ định nghĩa, tính chất và ứng dụng của phép quay sẽ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả và tự tin hơn. Hãy truy cập giaitoan.edu.vn để học tập và luyện tập ngay hôm nay!