Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 24 và 25 sách giáo khoa Toán 9 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Nhà may Hưng Thịnh tặng áo phông cho 40 học sinh của lớp 9A. Nhà may đo chiều cao (đơn vị: centimet) của cả lớp để quyết định chọn các cỡ áo khi may, kết quả như sau: a) Mẫu số liệu trên có bao nhiêu giá trị khác nhau? b) Có nên dùng bảng tần số (hay bảng tần số tương đối) để biểu diễn mẫu số liệu thống kê đó không?
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 24 SGK Toán 9 Cánh diều
Nhà may Hưng Thịnh tặng áo phông cho 40 học sinh của lớp 9A. Nhà may đo chiều cao (đơn vị: centimet) của cả lớp để quyết định chọn các cỡ áo khi may, kết quả như sau:

a) Mẫu số liệu trên có bao nhiêu giá trị khác nhau?
b) Có nên dùng bảng tần số (hay bảng tần số tương đối) để biểu diễn mẫu số liệu thống kê đó không?
Phương pháp giải:
a) Đếm các giá trị có trong bảng kết quả.
b) Bảng tần số (hay bảng tần số tương đối) không phù hợp với những kết quả điều tra, khảo sát có quá nhiều giá trị khác nhau.
Lời giải chi tiết:
a) Có các giá trị: 150; 152; 153; 156; 157; 158; 159; 160; 161; 163; 164; 165; 166; 167; 168; 169; 172; 174
Tổng: 18 giá trị khác nhau.
b) Không nên dùng bảng tần số (hay bảng tần số tương đối) vì có rất nhiều giá trị khác nhau nên bảng thống kê sẽ rất dài.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 25 SGK Toán 9 Cánh diều
Chiều cao (đơn vị: mét) của 35 cây bạch đàn được cho như sau:
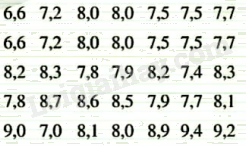
Hãy ghép các số liệu thành năm nhóm ứng với năm nửa khoảng có độ dài bằng nhau.
Phương pháp giải:
Bước 1: Xác định giá trị nhỏ nhất và giá trị lớn nhất trong mẫu số liệu.
Bước 2: Chọn nửa khoảng phù hợp và tính độ dài giữa 2 giá trị đó
Bước 3: Chia đều thành 5 nửa khoảng bằng nhau.
Lời giải chi tiết:
- Giá trị nhỏ nhất và giá trị lớn nhất trong mẫu số liệu là: 6,6 và 9,4.
- Chọn nửa khoảng [6,5; 9,5) có độ dài là 9,5 – 6,5 = 3.
Ta chia làm 5 nửa khoảng: [6,5; 7,1), [7,1; 7,7), [7,7; 8,3), [8,3; 8,9), [8,9; 9,5).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 24 SGK Toán 9 Cánh diều
Nhà may Hưng Thịnh tặng áo phông cho 40 học sinh của lớp 9A. Nhà may đo chiều cao (đơn vị: centimet) của cả lớp để quyết định chọn các cỡ áo khi may, kết quả như sau:

a) Mẫu số liệu trên có bao nhiêu giá trị khác nhau?
b) Có nên dùng bảng tần số (hay bảng tần số tương đối) để biểu diễn mẫu số liệu thống kê đó không?
Phương pháp giải:
a) Đếm các giá trị có trong bảng kết quả.
b) Bảng tần số (hay bảng tần số tương đối) không phù hợp với những kết quả điều tra, khảo sát có quá nhiều giá trị khác nhau.
Lời giải chi tiết:
a) Có các giá trị: 150; 152; 153; 156; 157; 158; 159; 160; 161; 163; 164; 165; 166; 167; 168; 169; 172; 174
Tổng: 18 giá trị khác nhau.
b) Không nên dùng bảng tần số (hay bảng tần số tương đối) vì có rất nhiều giá trị khác nhau nên bảng thống kê sẽ rất dài.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 25 SGK Toán 9 Cánh diều
Chiều cao (đơn vị: mét) của 35 cây bạch đàn được cho như sau:
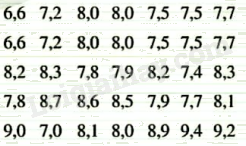
Hãy ghép các số liệu thành năm nhóm ứng với năm nửa khoảng có độ dài bằng nhau.
Phương pháp giải:
Bước 1: Xác định giá trị nhỏ nhất và giá trị lớn nhất trong mẫu số liệu.
Bước 2: Chọn nửa khoảng phù hợp và tính độ dài giữa 2 giá trị đó
Bước 3: Chia đều thành 5 nửa khoảng bằng nhau.
Lời giải chi tiết:
- Giá trị nhỏ nhất và giá trị lớn nhất trong mẫu số liệu là: 6,6 và 9,4.
- Chọn nửa khoảng [6,5; 9,5) có độ dài là 9,5 – 6,5 = 3.
Ta chia làm 5 nửa khoảng: [6,5; 7,1), [7,1; 7,7), [7,7; 8,3), [8,3; 8,9), [8,9; 9,5).
Mục 1 của chương trình Toán 9 tập 2 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong trang 24 và 25 SGK Toán 9 tập 2 - Cánh diều yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, tìm tọa độ đỉnh của parabol, vẽ đồ thị hàm số và xác định khoảng đồng biến, nghịch biến của hàm số. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc hai, công thức tính tọa độ đỉnh và các tính chất của parabol.
Bài 2 tập trung vào việc giải các phương trình bậc hai một ẩn. Học sinh cần sử dụng công thức nghiệm của phương trình bậc hai, điều kiện để phương trình có nghiệm và các phương pháp giải phương trình bậc hai như phương pháp phân tích thành nhân tử, phương pháp hoàn thiện bình phương và phương pháp sử dụng công thức nghiệm.
Bài 3 yêu cầu học sinh vận dụng kiến thức về phương trình bậc hai để giải các bài toán thực tế liên quan đến các lĩnh vực như vật lý, hình học và kinh tế. Để giải bài tập này, học sinh cần phân tích đề bài, xây dựng phương trình bậc hai và giải phương trình để tìm ra nghiệm.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 24 và 25 SGK Toán 9 tập 2 - Cánh diều:
Khi giải các bài tập trong mục 1 trang 24 và 25 SGK Toán 9 tập 2 - Cánh diều, học sinh cần lưu ý những điều sau:
Ngoài SGK Toán 9 tập 2 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với hướng dẫn chi tiết và đầy đủ này, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 1 trang 24 và 25 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!