Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 41 SGK Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Sau khi thống kê độ dài (đơn vị: centimet) của 50 cây con ở vườn thì nghiệm, người ta nhận được bảng tần số tương đối ghép nhóm như sau: Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm ở Bảng 38.
Đề bài
Sau khi thống kê độ dài (đơn vị: centimet) của 50 cây con ở vườn thì nghiệm, người ta nhận được bảng tần số tương đối ghép nhóm như sau:

Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm ở Bảng 38.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
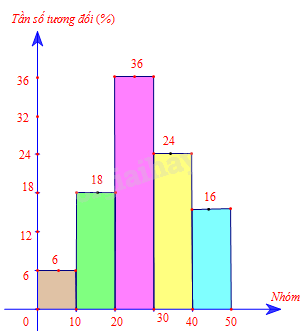
Biểu đồ cột: trục nằm ngang thể hiện các số liệu của các nhóm, trục thẳng đứng thể hiện tần số tương đối.
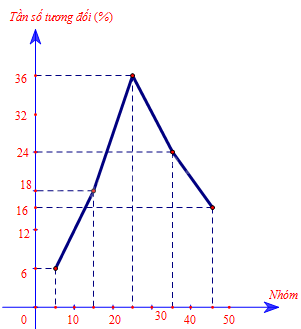
Biểu đồ đoạn thẳng: xác định các điểm \({M_1}({c_1};{f_1})\),\({M_2}({c_2};{f_2}),{M_3}({c_3};{f_3}),{M_4}({c_4};{f_4})\) trong đó \({c_1},{c_2},{c_3},{c_4}\)lần lượt là trung bình cộng hai đầu mút của nhóm 1, 2, 3, 4.
Lời giải chi tiết
Biểu đồ đoạn thẳng:
Biểu đồ cột:
Bài tập 4 trang 41 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình đại số, tập trung vào việc giải phương trình bậc hai một ẩn. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức về công thức nghiệm của phương trình bậc hai, điều kiện xác định của nghiệm và các phương pháp giải phương trình như phân tích thành nhân tử, sử dụng công thức nghiệm tổng quát, hoặc phương pháp hoàn thiện bình phương.
Bài tập 4 thường bao gồm một số phương trình bậc hai khác nhau, yêu cầu học sinh tìm nghiệm của phương trình. Các phương trình có thể có dạng tổng quát ax2 + bx + c = 0, với a, b, c là các hệ số thực và a ≠ 0. Việc xác định đúng các hệ số a, b, c là bước quan trọng để áp dụng đúng công thức nghiệm.
Ví dụ: Giải phương trình 2x2 - 5x + 2 = 0
Giải:
Vậy phương trình 2x2 - 5x + 2 = 0 có hai nghiệm là x1 = 2 và x2 = 0.5
Để củng cố kiến thức và kỹ năng giải phương trình bậc hai, bạn có thể luyện tập thêm với các bài tập sau:
Việc nắm vững phương pháp giải phương trình bậc hai là nền tảng quan trọng cho việc học các kiến thức toán học nâng cao hơn, đặc biệt là trong các lĩnh vực như vật lý, kỹ thuật và kinh tế. Khả năng giải quyết các bài toán liên quan đến phương trình bậc hai cũng giúp bạn phát triển tư duy logic và khả năng giải quyết vấn đề.
Giaitoan.edu.vn cam kết cung cấp những lời giải chính xác, dễ hiểu và đầy đủ, giúp bạn học Toán 9 một cách hiệu quả nhất. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác.