Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3 trang 124 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án và cách giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 3 thuộc chương trình học Toán 9 tập 1, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi hy vọng với những hướng dẫn chi tiết này, các em sẽ hiểu rõ hơn về phương pháp giải và áp dụng thành công vào các bài tập tương tự.
Cho hình vuông (ABCD) cạnh (r) và đường tròn (left( {C;r} right)) giả sử (M) là một điểm nằm trên đường tròn (left( {C;r} right)) sao cho điểm (M) nằm trong hình vuông (ABCD). Tiếp tuyến của đường tròn (left( {C;r} right)) tại tiếp điểm (M) cắt các đoạn thẳng (AB,AD) lần lượt tại (N,P). Chứng minh: a) Các đường thẳng (NB,PD) là các tiếp tuyến của đường tròn (left( {C;r} right)). b) (widehat {NCP} = widehat {NCB} + widehat {PCD} = 45^circ ).
Đề bài
Cho hình vuông \(ABCD\) cạnh \(r\) và đường tròn \(\left( {C;r} \right)\) giả sử \(M\) là một điểm nằm trên đường tròn \(\left( {C;r} \right)\) sao cho điểm \(M\) nằm trong hình vuông \(ABCD\). Tiếp tuyến của đường tròn \(\left( {C;r} \right)\) tại tiếp điểm \(M\) cắt các đoạn thẳng \(AB,AD\) lần lượt tại \(N,P\). Chứng minh:
a) Các đường thẳng \(NB,PD\) là các tiếp tuyến của đường tròn \(\left( {C;r} \right)\).
b) \(\widehat {NCP} = \widehat {NCB} + \widehat {PCD} = 45^\circ \).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đã học để chứng minh.
Lời giải chi tiết
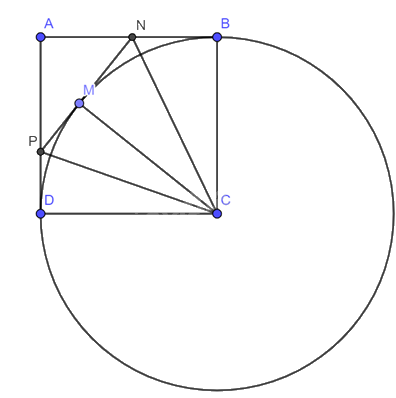
a) Do \(ABCD\) là hình vuông nên \(AB = BC = CD = AD = r\); \(AB \bot BC\) hay \(NB \bot BC\); \(AD \bot CD\) hay \(PD \bot CD\).
Xét \(\left( C \right)\) có:
+ \(B \in \left( C \right);NB \bot BC \Rightarrow NB\) là tiếp tuyến của \(\left( C \right)\).
+ \(D \in \left( C \right);PD \bot CD \Rightarrow PD\) là tiếp tuyến của \(\left( C \right)\).
b) Do \(MP\) và \(PD\) là hai tiếp tuyến cắt nhau tại \(P\) nên \(CP\) là tia phân giác của \(\widehat {MCD} \Rightarrow \widehat {MCP} = \widehat {PCD}\) (1).
Do \(MN\) nà \(NB\) là hai tiếp tuyến cắt nhau tại \(N\) nên \(CN\) là tia phân giác của \(\widehat {MCB} \Rightarrow \widehat {MCN} = \widehat {BCN}\)(2).
Từ (1) và (2) suy ra \(\widehat {MCP} + \widehat {MCN} = \widehat {PCD} + \widehat {BCN}\) \( \Rightarrow \widehat {PCN} = \widehat {PCD} + \widehat {BCN}\).
Lại có: \(\widehat {PCN} + \widehat {PCD} + \widehat {PCN} = 90^\circ \) hay \(\widehat {PCN} + \widehat {PCN} = 90^\circ \Rightarrow \widehat {PCN} = 45^\circ \).
Vậy \(\widehat {PCN} = \widehat {PCD} + \widehat {BCN} = 45^\circ \).
Bài tập 3 trang 124 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 9, yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Bài tập 3: Cho hàm số y = 2x + 3. Tìm giá trị của x khi y = 7.
Lời giải:
Để tìm giá trị của x khi y = 7, ta thay y = 7 vào phương trình hàm số và giải phương trình:
7 = 2x + 3
2x = 7 - 3
2x = 4
x = 2
Vậy, khi y = 7 thì x = 2.
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể tự giải các bài tập tương tự sau:
Kiến thức về hàm số bậc nhất và hàm số bậc hai có ứng dụng rất lớn trong thực tế, ví dụ như:
Để học tốt môn Toán 9, các em cần:
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!