Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 71, 72, 73 sách giáo khoa Toán 9 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
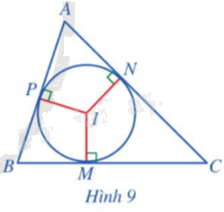
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 72SGK Toán 9 Cánh diều
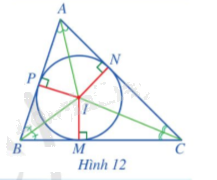
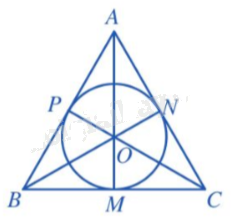
Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).
a) So sánh các đoạn thẳng IM, IN, IP.
b) Đặt r = IM. Đường tròn (I; r) có phải là đường tròn nội tiếp tam giác ABC hay không? Vì sao?
Phương pháp giải:
a) Áp dụng tính chất 3 đường phân giác trong tam giác.
b) Chứng minh IM = IN = IP = r.
Lời giải chi tiết:
a) Do I là giao của 3 đường phân giác trong tam giác ABC nên I cách đều 3 cạnh của tam giác, do đó IM = IN = IP.
b) Vì r = IM, mà IM = IN = IP nên IM = IN = IP = r.
Vậy đường tròn (I; r) là đường tròn nội tiếp tam giác ABC
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 71SGK Toán 9 Cánh diều
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
Phương pháp giải:
Các vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I) gồm: cắt nhau tại 2 điểm, tiếp xúc nhau (cắt nhau tại 1 điểm), không cắt nhau.
Lời giải chi tiết:
Các đường thẳng AB, BC, CA tiếp xúc với đường tròn (I) lần lượt tại các điểm: P, M, N.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 7 trang 73 SGK Toán 9 Cánh diều
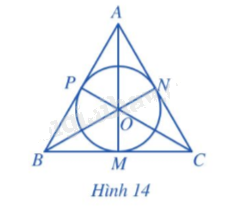
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 14).
a) AM, BN, CP có là các đường phân giác của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn nội tiếp tam giác ABC hay không?
c) Tính OM theo a.
Phương pháp giải:
a) Áp dụng: Trong tam giác cân, đường trung tuyến đồng thời là đường phân giác.
b) Chứng minh OM = ON = OP.
c) Áp dụng Pytago trong tam giác AMB vuông tại M.
Lời giải chi tiết:
a) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP đồng thời là ba đường phân giác.
b) Do O là giao của 3 đường phân giác trong tam giác ABC nên O cách đều 3 cạnh của tam giác, do đó OM = ON = OP.
Vậy đường tròn (O) là đường tròn nội tiếp tam giác ABC.
c) Xét tam giác ABC đều có đường trung tuyến AM nên \(BM = \frac{{BC}}{2} = \frac{a}{2}\) và AM đồng thời là đường cao, do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác AMB vuông tại M có:
\(AM = \sqrt {A{B^2} - B{M^2}} \) (Pytago).
Nên \(AM = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt 3 a}}{2}.\)
Mà \(OM = \frac{1}{3}AM\)(do AM là đường trung tuyến trong tam giác ABC).
Suy ra \(OM = \frac{1}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{6}.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 71SGK Toán 9 Cánh diều
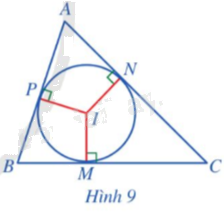
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
Phương pháp giải:
Các vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I) gồm: cắt nhau tại 2 điểm, tiếp xúc nhau (cắt nhau tại 1 điểm), không cắt nhau.
Lời giải chi tiết:
Các đường thẳng AB, BC, CA tiếp xúc với đường tròn (I) lần lượt tại các điểm: P, M, N.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 72SGK Toán 9 Cánh diều
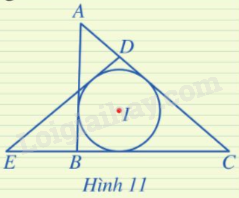
Trong Hình 11, đường tròn (I) là đường tròn nội tiếp những tam giác nào?
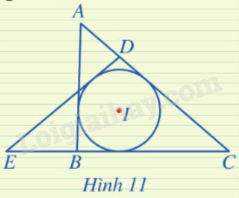
Phương pháp giải:
Xác định (I) tiếp xúc với các cạnh thuộc tam giác nào.
Lời giải chi tiết:
Đường tròn (I) là đường tròn nội tiếp tam giác ABC vì nó tiếp xúc với ba cạnh AB, BC, CA.
Đường tròn (I) là đường tròn nội tiếp tam giác CDE vì nó tiếp xúc với ba cạnh DE, DC, EC.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 72SGK Toán 9 Cánh diều
Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).
a) So sánh các đoạn thẳng IM, IN, IP.
b) Đặt r = IM. Đường tròn (I; r) có phải là đường tròn nội tiếp tam giác ABC hay không? Vì sao?
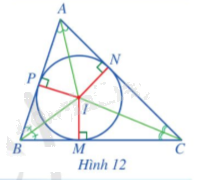
Phương pháp giải:
a) Áp dụng tính chất 3 đường phân giác trong tam giác.
b) Chứng minh IM = IN = IP = r.
Lời giải chi tiết:
a) Do I là giao của 3 đường phân giác trong tam giác ABC nên I cách đều 3 cạnh của tam giác, do đó IM = IN = IP.
b) Vì r = IM, mà IM = IN = IP nên IM = IN = IP = r.
Vậy đường tròn (I; r) là đường tròn nội tiếp tam giác ABC
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 7 trang 73 SGK Toán 9 Cánh diều
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 14).
a) AM, BN, CP có là các đường phân giác của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn nội tiếp tam giác ABC hay không?
c) Tính OM theo a.
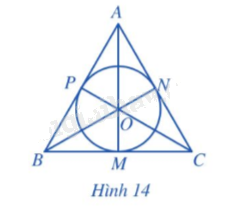
Phương pháp giải:
a) Áp dụng: Trong tam giác cân, đường trung tuyến đồng thời là đường phân giác.
b) Chứng minh OM = ON = OP.
c) Áp dụng Pytago trong tam giác AMB vuông tại M.
Lời giải chi tiết:
a) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP đồng thời là ba đường phân giác.
b) Do O là giao của 3 đường phân giác trong tam giác ABC nên O cách đều 3 cạnh của tam giác, do đó OM = ON = OP.
Vậy đường tròn (O) là đường tròn nội tiếp tam giác ABC.
c) Xét tam giác ABC đều có đường trung tuyến AM nên \(BM = \frac{{BC}}{2} = \frac{a}{2}\) và AM đồng thời là đường cao, do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác AMB vuông tại M có:
\(AM = \sqrt {A{B^2} - B{M^2}} \) (Pytago).
Nên \(AM = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt 3 a}}{2}.\)
Mà \(OM = \frac{1}{3}AM\)(do AM là đường trung tuyến trong tam giác ABC).
Suy ra \(OM = \frac{1}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{6}.\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 73 SGK Toán 9 Cánh diều
Cho tam giác đều ABC ngoại tiếp đường tròn (O; 6). Tính AB.
Phương pháp giải:
Dựa vào kiến thức về bán kính đường tròn nội tiếp để tính độ dài cạnh.
Lời giải chi tiết:
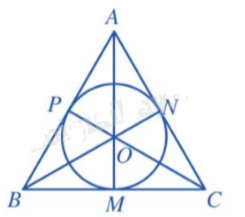
Gọi độ dài cạnh của tam giác ABC là a (cm), suy ra AB = a (cm)
Đường tròn (O; 6) nội tiếp tam giác ABC nên:
\(r = \frac{a \sqrt 3}{6}\)
hay \(6 = \frac{a \sqrt 3}{6}\)
Suy ra \(a = 6: \frac{\sqrt 3}{6} = 12\sqrt 3\)
Vậy \(AB = 12\sqrt 3 .\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 73 SGK Toán 9 Cánh diều
Cho tam giác đều ABC ngoại tiếp đường tròn (O; 6). Tính AB.
Phương pháp giải:
Dựa vào kiến thức về bán kính đường tròn nội tiếp để tính độ dài cạnh.
Lời giải chi tiết:
Gọi độ dài cạnh của tam giác ABC là a (cm), suy ra AB = a (cm)
Đường tròn (O; 6) nội tiếp tam giác ABC nên:
\(r = \frac{a \sqrt 3}{6}\)
hay \(6 = \frac{a \sqrt 3}{6}\)
Suy ra \(a = 6: \frac{\sqrt 3}{6} = 12\sqrt 3\)
Vậy \(AB = 12\sqrt 3 .\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 72SGK Toán 9 Cánh diều
Trong Hình 11, đường tròn (I) là đường tròn nội tiếp những tam giác nào?
Phương pháp giải:
Xác định (I) tiếp xúc với các cạnh thuộc tam giác nào.
Lời giải chi tiết:
Đường tròn (I) là đường tròn nội tiếp tam giác ABC vì nó tiếp xúc với ba cạnh AB, BC, CA.
Đường tròn (I) là đường tròn nội tiếp tam giác CDE vì nó tiếp xúc với ba cạnh DE, DC, EC.
Mục 2 của chương trình Toán 9 tập 2 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh nhắc lại các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của hàm số bậc hai, đồng thời biết cách áp dụng chúng vào việc giải quyết các bài toán cụ thể.
Bài tập này yêu cầu học sinh giải các phương trình bậc hai một ẩn bằng các phương pháp khác nhau, bao gồm:
Khi giải phương trình bậc hai, học sinh cần chú ý đến điều kiện xác định của phương trình và kiểm tra lại nghiệm để đảm bảo tính chính xác.
Bài tập này yêu cầu học sinh vận dụng kiến thức về phương trình bậc hai để giải quyết các bài toán thực tế, chẳng hạn như:
Để giải quyết các bài toán này, học sinh cần đọc kỹ đề bài, xác định các đại lượng liên quan và thiết lập phương trình bậc hai phù hợp.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 71, 72, 73 SGK Toán 9 tập 2 - Cánh diều:
(Giải chi tiết bài 1)
(Giải chi tiết bài 2)
(Giải chi tiết bài 3)
Để giải các bài tập về hàm số bậc hai và phương trình bậc hai một ẩn một cách hiệu quả, học sinh có thể tham khảo một số mẹo sau:
Hy vọng rằng với lời giải chi tiết và các mẹo giải toán hiệu quả mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 71, 72, 73 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!