Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 106 và 107 sách giáo khoa Toán 9 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
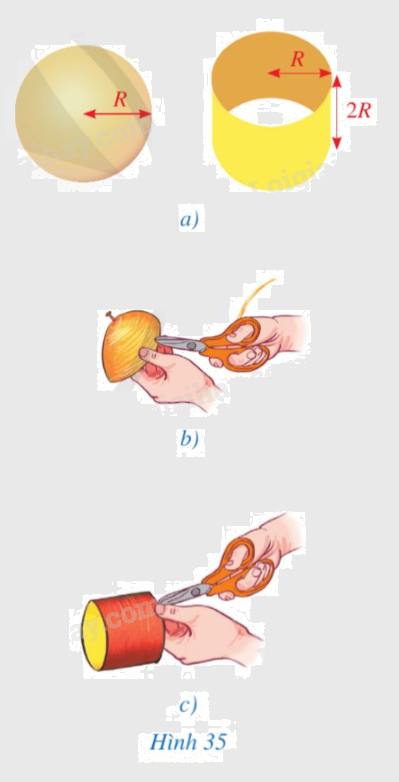
Thực hiện các hoạt động sau: a) Chuẩn bị một mặt cầu bằng nhựa (chẳng hạn quả bóng bằng nhựa mỏng) có bán kính là R và một hình trụ bằng bìa cứng (hoặc nhựa mỏng) có bán kính đáy là R và chiều cao là 2R (như Hình 35a) một cuộn dây mảnh, không dãn (chẳng hạn dây len) đủ dài. b) Dùng cuộn dây đó cuốn dần dần để phủ kín một nửa mặt cầu rồi cắt dây ở điểm cuối cùng (Hình 35b). Như vậy đoạn dây thứ nhất “đã lát kín” một nửa mặt cầu. Tiếp tục dùng cuộn dây đó cuốn dần dần để phủ kín mặt xung quanh
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 107SGK Toán 9 Cánh diều
Một quả bóng đá theo tiêu chuẩn chuyên nghiệp (cho cả nam và nữ, từ khoảng 11, 12 tuổi trở lên), thường nặng khoảng 450 g, có chu vi đường tròn lớn khoảng 70 cm. Diện tích bề mặt của quả bóng đá như thế bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải:
Từ công thức tính chu vi đường tròn \(C = \pi 2R\), ta tính được bán kính R của quả bóng.
Áp dụng công thức tính diện tích mặt cầu (\(S = 4\pi {R^2}\)) để tính diện tích bề mặt quả bóng.
Lời giải chi tiết:
Ta có: \(C = \pi 2R\) nên bán kính quả bóng là:
\(R = \frac{C}{{2\pi }} = \frac{{70}}{{2\pi }} = \frac{{35}}{\pi }\left( {cm} \right).\)
Diện tích bề mặt quả bóng là:
\(S = 4\pi {R^2} = 4\pi {\frac{{35}}{{{\pi ^2}}}^2} \approx 1560,51\left( {c{m^2}} \right).\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 106 SGK Toán 9 Cánh diều
Thực hiện các hoạt động sau:
a) Chuẩn bị một mặt cầu bằng nhựa (chẳng hạn quả bóng bằng nhựa mỏng) có bán kính là R và một hình trụ bằng bìa cứng (hoặc nhựa mỏng) có bán kính đáy là R và chiều cao là 2R (như Hình 35a) một cuộn dây mảnh, không dãn (chẳng hạn dây len) đủ dài.
b) Dùng cuộn dây đó cuốn dần dần để phủ kín một nửa mặt cầu rồi cắt dây ở điểm cuối cùng (Hình 35b). Như vậy đoạn dây thứ nhất “đã lát kín” một nửa mặt cầu. Tiếp tục dùng cuộn dây đó cuốn dần dần để phủ kín mặt xung quanh của hình trụ và cắt dây ở điểm cuối cùng (Hình 35c). Ta được đoạn dây thứ hai “lát kín” mặt xung quanh của hình trụ đã cho.
Gỡ từng đoạn dây quấn quanh nửa mặt cầu và mặt xung quanh của hình trụ nói trên, ta thấy hai đoạn dây đó có độ dài bằng nhau.
Do hai đoạn dây lần lượt lát kín một nửa mặt cầu, mặt xung quanh của hình trụ và độ dài hai đoạn dây đó bằng nhau nên ta có thể coi hai mặt đó có diện tích bằng nhau.
c) Tính diện tích xung quanh của hình trụ có bán kính đáy là R và chiều cao là 2R. Từ đó, hãy nêu dự đoán về công thức tính diện tích của mặt cầu bán kính R.
Phương pháp giải:
a,b: Làm theo yêu cầu.
c) Áp dụng công thức tính diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\), dự đoán diện tích mặt cầu.
Lời giải chi tiết:
a) Chuẩn bị các vật thể: quả bóng bàn, hình trụ theo kích thước của quả bóng, cuộn dây.
b) Đánh dấu 1 nửa hình cầu, cuốn dây để lát kính nửa mặt cầu đó.
Dùng đoạn dây khác lát kín mặt xung quanh của hình trụ.
Gỡ 2 đoạn dây đó và thấy độ dài 2 đoạn dây bằng nhau nên hai mặt đó có diện tích bằng nhau.
c) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .R.2R = 4\pi {R^2}.\)
Vì diện tích xung quanh của hình trụ bằng diện tích mặt cầu nên diện tích mặt cầu là \(S = 4\pi {R^2}.\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 107SGK Toán 9 Cánh diều
Một quả bóng đá theo tiêu chuẩn chuyên nghiệp (cho cả nam và nữ, từ khoảng 11, 12 tuổi trở lên), thường nặng khoảng 450 g, có chu vi đường tròn lớn khoảng 70 cm. Diện tích bề mặt của quả bóng đá như thế bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải:
Từ công thức tính chu vi đường tròn \(C = \pi 2R\), ta tính được bán kính R của quả bóng.
Áp dụng công thức tính diện tích mặt cầu (\(S = 4\pi {R^2}\)) để tính diện tích bề mặt quả bóng.
Lời giải chi tiết:
Ta có: \(C = \pi 2R\) nên bán kính quả bóng là:
\(R = \frac{C}{{2\pi }} = \frac{{70}}{{2\pi }} = \frac{{35}}{\pi }\left( {cm} \right).\)
Diện tích bề mặt quả bóng là:
\(S = 4\pi {R^2} = 4\pi {\frac{{35}}{{{\pi ^2}}}^2} \approx 1560,51\left( {c{m^2}} \right).\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 106 SGK Toán 9 Cánh diều
Thực hiện các hoạt động sau:
a) Chuẩn bị một mặt cầu bằng nhựa (chẳng hạn quả bóng bằng nhựa mỏng) có bán kính là R và một hình trụ bằng bìa cứng (hoặc nhựa mỏng) có bán kính đáy là R và chiều cao là 2R (như Hình 35a) một cuộn dây mảnh, không dãn (chẳng hạn dây len) đủ dài.
b) Dùng cuộn dây đó cuốn dần dần để phủ kín một nửa mặt cầu rồi cắt dây ở điểm cuối cùng (Hình 35b). Như vậy đoạn dây thứ nhất “đã lát kín” một nửa mặt cầu. Tiếp tục dùng cuộn dây đó cuốn dần dần để phủ kín mặt xung quanh của hình trụ và cắt dây ở điểm cuối cùng (Hình 35c). Ta được đoạn dây thứ hai “lát kín” mặt xung quanh của hình trụ đã cho.
Gỡ từng đoạn dây quấn quanh nửa mặt cầu và mặt xung quanh của hình trụ nói trên, ta thấy hai đoạn dây đó có độ dài bằng nhau.
Do hai đoạn dây lần lượt lát kín một nửa mặt cầu, mặt xung quanh của hình trụ và độ dài hai đoạn dây đó bằng nhau nên ta có thể coi hai mặt đó có diện tích bằng nhau.
c) Tính diện tích xung quanh của hình trụ có bán kính đáy là R và chiều cao là 2R. Từ đó, hãy nêu dự đoán về công thức tính diện tích của mặt cầu bán kính R.

Phương pháp giải:
a,b: Làm theo yêu cầu.
c) Áp dụng công thức tính diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\), dự đoán diện tích mặt cầu.
Lời giải chi tiết:
a) Chuẩn bị các vật thể: quả bóng bàn, hình trụ theo kích thước của quả bóng, cuộn dây.
b) Đánh dấu 1 nửa hình cầu, cuốn dây để lát kính nửa mặt cầu đó.
Dùng đoạn dây khác lát kín mặt xung quanh của hình trụ.
Gỡ 2 đoạn dây đó và thấy độ dài 2 đoạn dây bằng nhau nên hai mặt đó có diện tích bằng nhau.
c) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .R.2R = 4\pi {R^2}.\)
Vì diện tích xung quanh của hình trụ bằng diện tích mặt cầu nên diện tích mặt cầu là \(S = 4\pi {R^2}.\)
Mục 2 trong SGK Toán 9 tập 2 - Cánh diều thường tập trung vào một chủ đề cụ thể, ví dụ như hàm số bậc hai, phương trình bậc hai, hoặc hệ phương trình. Việc nắm vững kiến thức nền tảng và phương pháp giải bài tập trong mục này là rất quan trọng để các em có thể giải quyết các bài toán phức tạp hơn trong các chương tiếp theo.
Để giúp các em hiểu rõ hơn về nội dung bài học, chúng tôi sẽ giải chi tiết từng bài tập trong mục 2 trang 106 và 107. Mỗi bài giải sẽ bao gồm:
Đề bài: Cho hàm số y = ax2 + bx + c. Tìm a, b, c biết đồ thị hàm số đi qua các điểm A(0; 1), B(1; 2), C(-1; 0).
Lời giải:
Đề bài: Giải phương trình bậc hai 2x2 - 5x + 3 = 0.
Lời giải:
Phương trình có dạng ax2 + bx + c = 0 với a = 2, b = -5, c = 3.
Tính delta: Δ = b2 - 4ac = (-5)2 - 4(2)(3) = 25 - 24 = 1.
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-b + √Δ) / 2a = (5 + 1) / (2*2) = 3/2
x2 = (-b - √Δ) / 2a = (5 - 1) / (2*2) = 1
Vậy phương trình có hai nghiệm x1 = 3/2 và x2 = 1.
Để giải bài tập Toán 9 tập 2 - Cánh diều một cách hiệu quả, các em cần:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 106, 107 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!