Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho bài tập 1 trang 124 SGK Toán 9 tập 1, sách Cánh diều. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán Toán 9.
Trong Hình 92, cho các điểm (A,B,C,D,E) thuộc đường tròn (left( O right)). a) Số đo góc (BOC) là: A. (alpha ) B. (2alpha ) C. (180^circ - alpha ) B. (180^circ - 2alpha ) b) Số đo góc (BDC) là: A. (alpha ) B. (frac{alpha }{2}) C. (180^circ - alpha ) D. (180^circ - frac{alpha }{2}) c) Số đo góc (BEC) là: A. (alpha ) B. (2alpha ) C. (180^circ - alpha ) D. (360^circ - alpha )
Đề bài
Trong Hình 92, cho các điểm \(A,B,C,D,E\) thuộc đường tròn \(\left( O \right)\).
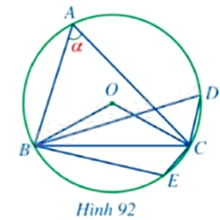
a) Số đo góc \(BOC\) là:
A. \(\alpha \)
B. \(2\alpha \)
C. \(180^\circ - \alpha \)
B. \(180^\circ - 2\alpha \)
b) Số đo góc \(BDC\) là:
A. \(\alpha \)
B. \(\frac{\alpha }{2}\)
C. \(180^\circ - \alpha \)
D. \(180^\circ - \frac{\alpha }{2}\)
c) Số đo góc \(BEC\) là:
A. \(\alpha \)
B. \(2\alpha \)
C. \(180^\circ - \alpha \)
D. \(360^\circ - \alpha \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào mối liên hệ giữa góc nội tiếp đường tròn và góc ở tâm để tính.
Lời giải chi tiết
a) Do \(\widehat {BOC}\) là góc ở tâm chắn cung $\overset\frown{BC}$, \(\widehat {BAC}\) là góc nội tiếp chắn cung $\overset\frown{BC}$ nên \(\widehat {BOC} = 2\widehat {BAC} = 2\alpha \).
Chọn đáp án B.
b) Do \(\widehat {BDC}\) là góc nội tiếp chắn cung $\overset\frown{BC}$, \(\widehat {BAC}\) là góc nội tiếp chắn cung $\overset\frown{BC}$ nên \(\widehat {BAC} = \widehat {BDC} = \alpha \).
Chọn đáp án A.
c) Do \(\widehat {BEC}\) là góc nội tiếp chắn cung lớn $\overset\frown{BC}$, \(\widehat {BAC}\) là góc nội tiếp chắn cung nhỏ $\overset\frown{BC}$ nên \(\widehat {BEC} = \frac{1}{2}\left( {360^\circ - 2\alpha } \right) = 180^\circ - \alpha \).
Chọn đáp án C.
Bài tập 1 trang 124 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và đường thẳng song song, vuông góc. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài tập 1 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài tập 1 trang 124 SGK Toán 9 tập 1 - Cánh diều một cách hiệu quả, học sinh cần:
Câu a: Xác định hệ số góc của đường thẳng y = 2x - 3.
Lời giải: Hệ số góc của đường thẳng y = 2x - 3 là a = 2.
Câu b: Xác định đường thẳng song song với đường thẳng y = -x + 1.
Lời giải: Đường thẳng song song với đường thẳng y = -x + 1 có hệ số góc là a = -1. Ví dụ, đường thẳng y = -x + 2 là một đường thẳng song song với đường thẳng y = -x + 1.
Câu c: Xác định đường thẳng vuông góc với đường thẳng y = 3x + 5.
Lời giải: Đường thẳng vuông góc với đường thẳng y = 3x + 5 có hệ số góc là a = -1/3. Ví dụ, đường thẳng y = (-1/3)x + 1 là một đường thẳng vuông góc với đường thẳng y = 3x + 5.
Để củng cố kiến thức về hàm số bậc nhất và các điều kiện song song, vuông góc, các em có thể tự giải các bài tập sau:
Bài tập 1 trang 124 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán Toán 9.
| Bài tập | Nội dung | Lời giải |
|---|---|---|
| 1a | Xác định hệ số góc y = 2x - 3 | a = 2 |
| 1b | Đường thẳng song song y = -x + 1 | y = -x + 2 (ví dụ) |
| 1c | Đường thẳng vuông góc y = 3x + 5 | y = (-1/3)x + 1 (ví dụ) |