Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 106, 107 sách giáo khoa Toán 9 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho đường thẳng (a) là tiếp tuyến của đường tròn (left( {O;R} right)). Gọi (H) là hình chiếu của tâm (O) trên đường thẳng (a) (Hình 33). a) So sánh khoảng cách (OH) từ tâm (O) đến đường thẳng (a) và bán kính (R). b) Điểm (H) có thuộc đường tròn (left( {O;R} right)) hay không? c) Điểm (H) có phải là tiếp điểm của đường thẳng (a) và đường tròn (left( {O;R} right)) hay không? d) Đường thẳng (a) có vuông góc với bán kính đi qua tiếp điểm hay không?
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 106 SGK Toán 9 Cánh diều
Cho đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\). Gọi \(H\) là hình chiếu của tâm \(O\) trên đường thẳng \(a\) (Hình 33).
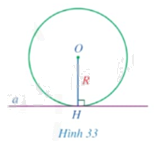
a) So sánh khoảng cách \(OH\) từ tâm \(O\) đến đường thẳng \(a\) và bán kính \(R\).
b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
c) Điểm \(H\) có phải là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) hay không?
d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm hay không?
Phương pháp giải:
Dựa vào hình ảnh trực quan để trả lời câu hỏi.
Lời giải chi tiết:
a) \(OH = R\).
b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\).
c) Điểm \(H\) là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\).
d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 107 SGK Toán 9 Cánh diều
Cho ba điểm \(A,B,C\) thẳng hàng, trong đó \(B\) nằm giữa \(A\) và \(C\). Đường tròn \(\left( O \right)\) tiếp xúc với đường thẳng \(AB\) tại điểm \(C\). Chứng minh: \(A{O^2} + B{C^2} = B{O^2} + A{C^2}\).
Phương pháp giải:
Dựa vào kiến thức vừa học để chứng minh.
Lời giải chi tiết:
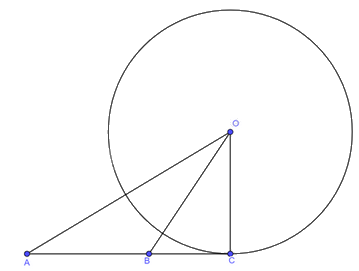
Vì đường thẳng \(AB\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(C\) nên \(OC \bot AB\). Suy ra tam giác \(OBC\) vuông tại \(C\), tam giác \(OAC\) vuông tại C.
Áp dụng định lý Pythagore vào tam giác \(OAC\) vuông tại \(C\), ta có:
\(O{A^2} = O{C^2} + A{C^2} \Rightarrow O{C^2} = O{A^2} - A{C^2}\,\,\left( 1 \right)\).
Áp dụng định lý Pythagore vào tam giác \(OBC\) vuông tại \(C\), ta có:
\(O{B^2} = O{C^2} + B{C^2} \Rightarrow O{C^2} = O{B^2} - B{C^2}\,\,\,\left( 2 \right)\).
Từ (1) và (2) suy ra \(O{A^2} - A{C^2} = O{B^2} - B{C^2} \Rightarrow O{A^2} + B{C^2} = O{B^2} + A{C^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 107 SGK Toán 9 Cánh diều
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) tiếp xúc ngoài nhau tại điểm \(I\). Gọi \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\). Chứng minh \(d\) là tiếp tuyến của \(\left( {O';R'} \right)\).
Phương pháp giải:
Dựa vào kiến thức vừa học để chứng minh.
Lời giải chi tiết:
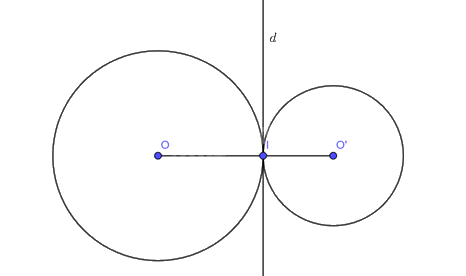
Vì (O;R) và (O';R') tiếp xúc ngoài nhau tại I nên O, I, O' thẳng hàng và I nằm giữa O và O'.
Do \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\) nên \(OI \bot d\) hay \(O'I \bot d\).
Mà \(I \in \left( {O'} \right),I \in d\) nên \(d\) là tiếp tuyến của \(\left( {O';R'} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 108 SGK Toán 9 Cánh diều
Cho hai đường tròn \(\left( O \right),\left( {O'} \right)\) cắt nhau tại hai điểm \(A,B\) sao cho đường thẳng \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\). Chứng minh đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Phương pháp giải:
Dựa vào các kiến thức vừa học để chứng minh.
Lời giải chi tiết:
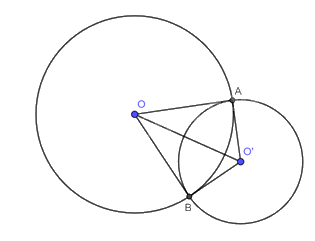
Do \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\) nên \(O'A \bot OA\). Vậy \(\widehat {OAO'} = 90^\circ \).
Xét tam giác \(OAO'\) và tam giác \(OBO'\) có:
\(\left\{ \begin{array}{l}O'A = O'B\\OO'\,\,chung\\OA = OB\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \Delta OAO' = \Delta OBO'\left( {c.c.c} \right)\\ \Rightarrow \widehat {OAO'} = \widehat {OBO'}\end{array}\).
Mà \(\widehat {OAO'} = 90^\circ \) nên \(\widehat {OBO'} = 90^\circ \) hay \(OB \bot O'B\).
Vậy đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 107SGK Toán 9 Cánh diều
Cho đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) thỏa mãn đường thẳng \(a\) đi qua điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) và \(a \bot OH\).
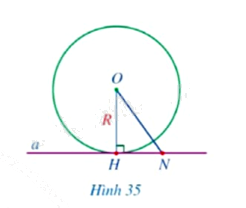
a) So sánh khoảng cách từ điểm \(O\) đến đường thẳng \(a\) và bán kính \(R\).
b) Giả sử \(N\) là điểm thuộc đường thẳng \(a\) và \(N\) khác \(H\). So sánh \(ON\) và \(R\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
c) Đường thẳng \(a\) có phải là tiếp tuyến của đường tròn \(\left( {O;R} \right)\) hay không?
Phương pháp giải:
Dựa vào hình ảnh trực quan và các kiến thức đã học để trả lời câu hỏi.
Lời giải chi tiết:
a) Khoảng cách từ điểm \(O\) đến đường thẳng \(a\) là đoạn \(OH\).
Do điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) nên \(OH = R\).
Vậy khoảng cách từ điểm \(O\) đến đường thẳng \(a\) bằng bán kính \(R\).
b) Xét tam giác \(OHN\) vuông tại \(H\) có: \(ON\) là cạnh huyền, \(OH\) là cạnh góc vuông.
Suy ra \(ON > OH\), lại có \(OH = R\). Vậy \(ON > R\).
Điểm \(N\) không thuộc đường tròn \(\left( {O;R} \right)\).
c) Đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 106 SGK Toán 9 Cánh diều
Cho đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\). Gọi \(H\) là hình chiếu của tâm \(O\) trên đường thẳng \(a\) (Hình 33).
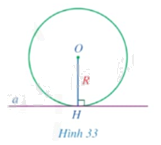
a) So sánh khoảng cách \(OH\) từ tâm \(O\) đến đường thẳng \(a\) và bán kính \(R\).
b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
c) Điểm \(H\) có phải là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) hay không?
d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm hay không?
Phương pháp giải:
Dựa vào hình ảnh trực quan để trả lời câu hỏi.
Lời giải chi tiết:
a) \(OH = R\).
b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\).
c) Điểm \(H\) là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\).
d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 107 SGK Toán 9 Cánh diều
Cho ba điểm \(A,B,C\) thẳng hàng, trong đó \(B\) nằm giữa \(A\) và \(C\). Đường tròn \(\left( O \right)\) tiếp xúc với đường thẳng \(AB\) tại điểm \(C\). Chứng minh: \(A{O^2} + B{C^2} = B{O^2} + A{C^2}\).
Phương pháp giải:
Dựa vào kiến thức vừa học để chứng minh.
Lời giải chi tiết:
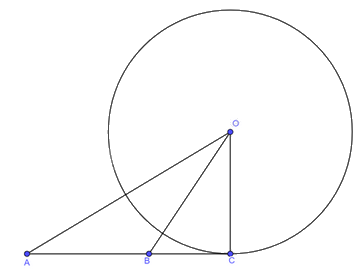
Vì đường thẳng \(AB\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(C\) nên \(OC \bot AB\). Suy ra tam giác \(OBC\) vuông tại \(C\), tam giác \(OAC\) vuông tại C.
Áp dụng định lý Pythagore vào tam giác \(OAC\) vuông tại \(C\), ta có:
\(O{A^2} = O{C^2} + A{C^2} \Rightarrow O{C^2} = O{A^2} - A{C^2}\,\,\left( 1 \right)\).
Áp dụng định lý Pythagore vào tam giác \(OBC\) vuông tại \(C\), ta có:
\(O{B^2} = O{C^2} + B{C^2} \Rightarrow O{C^2} = O{B^2} - B{C^2}\,\,\,\left( 2 \right)\).
Từ (1) và (2) suy ra \(O{A^2} - A{C^2} = O{B^2} - B{C^2} \Rightarrow O{A^2} + B{C^2} = O{B^2} + A{C^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 107SGK Toán 9 Cánh diều
Cho đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) thỏa mãn đường thẳng \(a\) đi qua điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) và \(a \bot OH\).
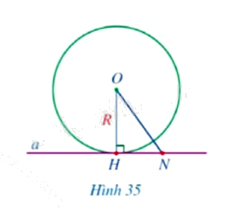
a) So sánh khoảng cách từ điểm \(O\) đến đường thẳng \(a\) và bán kính \(R\).
b) Giả sử \(N\) là điểm thuộc đường thẳng \(a\) và \(N\) khác \(H\). So sánh \(ON\) và \(R\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
c) Đường thẳng \(a\) có phải là tiếp tuyến của đường tròn \(\left( {O;R} \right)\) hay không?
Phương pháp giải:
Dựa vào hình ảnh trực quan và các kiến thức đã học để trả lời câu hỏi.
Lời giải chi tiết:
a) Khoảng cách từ điểm \(O\) đến đường thẳng \(a\) là đoạn \(OH\).
Do điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) nên \(OH = R\).
Vậy khoảng cách từ điểm \(O\) đến đường thẳng \(a\) bằng bán kính \(R\).
b) Xét tam giác \(OHN\) vuông tại \(H\) có: \(ON\) là cạnh huyền, \(OH\) là cạnh góc vuông.
Suy ra \(ON > OH\), lại có \(OH = R\). Vậy \(ON > R\).
Điểm \(N\) không thuộc đường tròn \(\left( {O;R} \right)\).
c) Đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 107 SGK Toán 9 Cánh diều
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) tiếp xúc ngoài nhau tại điểm \(I\). Gọi \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\). Chứng minh \(d\) là tiếp tuyến của \(\left( {O';R'} \right)\).
Phương pháp giải:
Dựa vào kiến thức vừa học để chứng minh.
Lời giải chi tiết:
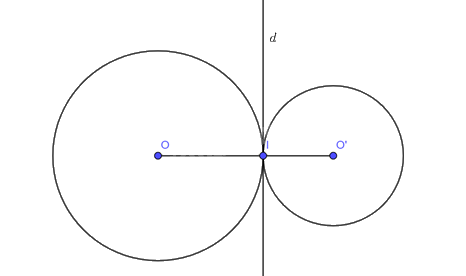
Vì (O;R) và (O';R') tiếp xúc ngoài nhau tại I nên O, I, O' thẳng hàng và I nằm giữa O và O'.
Do \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\) nên \(OI \bot d\) hay \(O'I \bot d\).
Mà \(I \in \left( {O'} \right),I \in d\) nên \(d\) là tiếp tuyến của \(\left( {O';R'} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 108 SGK Toán 9 Cánh diều
Cho hai đường tròn \(\left( O \right),\left( {O'} \right)\) cắt nhau tại hai điểm \(A,B\) sao cho đường thẳng \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\). Chứng minh đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Phương pháp giải:
Dựa vào các kiến thức vừa học để chứng minh.
Lời giải chi tiết:
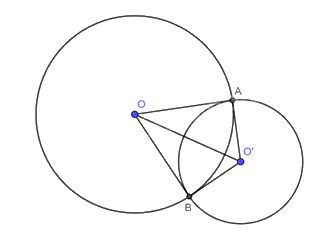
Do \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\) nên \(O'A \bot OA\). Vậy \(\widehat {OAO'} = 90^\circ \).
Xét tam giác \(OAO'\) và tam giác \(OBO'\) có:
\(\left\{ \begin{array}{l}O'A = O'B\\OO'\,\,chung\\OA = OB\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \Delta OAO' = \Delta OBO'\left( {c.c.c} \right)\\ \Rightarrow \widehat {OAO'} = \widehat {OBO'}\end{array}\).
Mà \(\widehat {OAO'} = 90^\circ \) nên \(\widehat {OBO'} = 90^\circ \) hay \(OB \bot O'B\).
Vậy đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Mục 1 trang 106, 107 SGK Toán 9 tập 1 - Cánh diều thường tập trung vào việc ôn tập và củng cố kiến thức về các dạng toán đã học trong chương. Các bài tập trong mục này thường mang tính tổng hợp, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết vấn đề.
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 1 trang 106, 107 SGK Toán 9 tập 1 - Cánh diều, chúng tôi sẽ phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh ôn lại các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Để giải bài tập này, học sinh cần nắm vững các khái niệm và công thức liên quan đến hàm số bậc nhất. Ngoài ra, học sinh cũng cần rèn luyện kỹ năng vẽ đồ thị hàm số và phân tích các tính chất của đồ thị.
Bài tập này yêu cầu học sinh giải các hệ phương trình bậc nhất hai ẩn bằng các phương pháp khác nhau, bao gồm:
Để giải bài tập này, học sinh cần nắm vững các bước giải hệ phương trình bằng các phương pháp trên. Ngoài ra, học sinh cũng cần rèn luyện kỹ năng biến đổi phương trình và tìm nghiệm của hệ phương trình.
Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế. Ví dụ, bài toán về tính quãng đường, thời gian, vận tốc, hoặc bài toán về tính lợi nhuận, chi phí, giá thành.
Để giải bài tập này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến hàm số bậc nhất, và xây dựng phương trình hàm số phù hợp. Sau đó, học sinh cần giải phương trình hàm số để tìm ra đáp án của bài toán.
Để giải bài tập mục 1 trang 106, 107 SGK Toán 9 tập 1 - Cánh diều một cách hiệu quả, các em nên:
Ngoài SGK Toán 9 tập 1 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để học tập và rèn luyện kỹ năng giải toán:
Hy vọng rằng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin giải quyết các bài tập trong mục 1 trang 106, 107 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!