Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 77, 78 SGK Toán 9 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập trong mục 2 tập trung vào các kiến thức quan trọng của chương trình Toán 9, đòi hỏi các em phải vận dụng linh hoạt các công thức và định lý đã học.
Cho tam giác (ABC) vuông tại (A) (Hình 7). a) Tổng số đo của góc (B) và góc (C) bằng bao nhiêu? b) Viết công thức tính các tỉ số lượng giác của góc (B) và góc (C). c) Mỗi tỉ số lượng giác của góc (B) bằng tỉ số lượng giác nào của góc (C)?
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 77SGK Toán 9 Cánh diều
Tính:
a) \(\sin 61^\circ - \cos 29^\circ \);
b) \(\cos 15^\circ - \sin 75^\circ \)
c) \(\tan 28^\circ - \cot 62^\circ \);
d) \(\cot 47^\circ - \tan 43^\circ \).
Phương pháp giải:
Dựa vào định lí về hai góc phụ nhau để giải bài toán.
Lời giải chi tiết:
a) Vì \(61^\circ \) và \(29^\circ \) là hai góc phụ nhau nên ta có: \(\sin 61^\circ = \cos 29^\circ \).
Vậy \(\sin 61^\circ - \cos 29^\circ = \cos 29^\circ - \cos 29^\circ = 0\).
b) Vì \(15^\circ \) và \(75^\circ \) là hai góc phụ nhau nên ta có: \(\cos 15^\circ = \sin 75^\circ \).
Vậy \(\cos 15^\circ - \sin 75^\circ = \sin 75^\circ - \sin 75^\circ = 0\).
c) Vì \(28^\circ \) và \(62^\circ \) là hai góc phụ nhau nên ta có: \(\tan 28^\circ = \cot 62^\circ \).
Vậy \(\tan 28^\circ - \cot 62^\circ = \cot 62^\circ - \cot 62^\circ = 0\).
d) Vì \(47^\circ \) và \(43^\circ \) là hai góc phụ nhau nên ta có: \(\cot 47^\circ = \tan 43^\circ \).
Vậy \(\cot 47^\circ - \tan 43^\circ = \tan 43^\circ - \tan 43^\circ = 0\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 78SGK Toán 9 Cánh diều
Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của biểu thức:
\(\sin 60^\circ - \cos 60^\circ .\tan 60^\circ \).
Phương pháp giải:
Dựa vào các giá trị đặc biệt của các góc để tính.
Lời giải chi tiết:
\(\sin 60^\circ - \cos 60^\circ .\tan 60^\circ = \frac{{\sqrt 3 }}{2} - \frac{1}{2}.\sqrt 3 = \frac{{\sqrt 3 }}{2} - \frac{{\sqrt 3 }}{2} = 0\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 77SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 7).
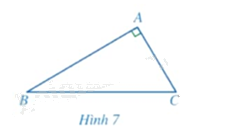
a) Tổng số đo của góc \(B\) và góc \(C\) bằng bao nhiêu?
b) Viết công thức tính các tỉ số lượng giác của góc \(B\) và góc \(C\).
c) Mỗi tỉ số lượng giác của góc \(B\) bằng tỉ số lượng giác nào của góc \(C\)?
Phương pháp giải:
Dựa vào kiến thức về tam giác vuông và tỉ số lượng giác để trả lời câu hỏi.
Lời giải chi tiết:
a) Tổng số đo của góc \(B\) và góc \(C\) bằng \(90^\circ \).
b) Do tam giác \(ABC\) vuông tại \(A\) nên:
+ \(\sin \widehat B = \frac{{AC}}{{BC}}\)
+ \(\cos \widehat B = \frac{{AB}}{{BC}}\)
+ \(\tan \widehat B = \frac{{AC}}{{AB}}\)
+ \(\cot \widehat B = \frac{{AB}}{{AC}}\)
+ \(\sin \widehat C = \frac{{AB}}{{BC}}\)
+ \(\cos \widehat C = \frac{{AC}}{{BC}}\)
+ \(\tan \widehat C = \frac{{AB}}{{AC}}\)
+ \(\cot \widehat C = \frac{{AC}}{{AB}}\)
c) \(\sin \widehat B = \cos \widehat C\)
\(\cos \widehat B = \sin \widehat C\)
\(\tan \widehat B = \cot \widehat C\)
\(\cot \widehat B = \tan \widehat C\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 77SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 7).
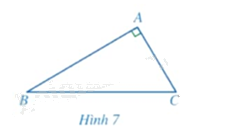
a) Tổng số đo của góc \(B\) và góc \(C\) bằng bao nhiêu?
b) Viết công thức tính các tỉ số lượng giác của góc \(B\) và góc \(C\).
c) Mỗi tỉ số lượng giác của góc \(B\) bằng tỉ số lượng giác nào của góc \(C\)?
Phương pháp giải:
Dựa vào kiến thức về tam giác vuông và tỉ số lượng giác để trả lời câu hỏi.
Lời giải chi tiết:
a) Tổng số đo của góc \(B\) và góc \(C\) bằng \(90^\circ \).
b) Do tam giác \(ABC\) vuông tại \(A\) nên:
+ \(\sin \widehat B = \frac{{AC}}{{BC}}\)
+ \(\cos \widehat B = \frac{{AB}}{{BC}}\)
+ \(\tan \widehat B = \frac{{AC}}{{AB}}\)
+ \(\cot \widehat B = \frac{{AB}}{{AC}}\)
+ \(\sin \widehat C = \frac{{AB}}{{BC}}\)
+ \(\cos \widehat C = \frac{{AC}}{{BC}}\)
+ \(\tan \widehat C = \frac{{AB}}{{AC}}\)
+ \(\cot \widehat C = \frac{{AC}}{{AB}}\)
c) \(\sin \widehat B = \cos \widehat C\)
\(\cos \widehat B = \sin \widehat C\)
\(\tan \widehat B = \cot \widehat C\)
\(\cot \widehat B = \tan \widehat C\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 77SGK Toán 9 Cánh diều
Tính:
a) \(\sin 61^\circ - \cos 29^\circ \);
b) \(\cos 15^\circ - \sin 75^\circ \)
c) \(\tan 28^\circ - \cot 62^\circ \);
d) \(\cot 47^\circ - \tan 43^\circ \).
Phương pháp giải:
Dựa vào định lí về hai góc phụ nhau để giải bài toán.
Lời giải chi tiết:
a) Vì \(61^\circ \) và \(29^\circ \) là hai góc phụ nhau nên ta có: \(\sin 61^\circ = \cos 29^\circ \).
Vậy \(\sin 61^\circ - \cos 29^\circ = \cos 29^\circ - \cos 29^\circ = 0\).
b) Vì \(15^\circ \) và \(75^\circ \) là hai góc phụ nhau nên ta có: \(\cos 15^\circ = \sin 75^\circ \).
Vậy \(\cos 15^\circ - \sin 75^\circ = \sin 75^\circ - \sin 75^\circ = 0\).
c) Vì \(28^\circ \) và \(62^\circ \) là hai góc phụ nhau nên ta có: \(\tan 28^\circ = \cot 62^\circ \).
Vậy \(\tan 28^\circ - \cot 62^\circ = \cot 62^\circ - \cot 62^\circ = 0\).
d) Vì \(47^\circ \) và \(43^\circ \) là hai góc phụ nhau nên ta có: \(\cot 47^\circ = \tan 43^\circ \).
Vậy \(\cot 47^\circ - \tan 43^\circ = \tan 43^\circ - \tan 43^\circ = 0\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 78SGK Toán 9 Cánh diều
Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của biểu thức:
\(\sin 60^\circ - \cos 60^\circ .\tan 60^\circ \).
Phương pháp giải:
Dựa vào các giá trị đặc biệt của các góc để tính.
Lời giải chi tiết:
\(\sin 60^\circ - \cos 60^\circ .\tan 60^\circ = \frac{{\sqrt 3 }}{2} - \frac{1}{2}.\sqrt 3 = \frac{{\sqrt 3 }}{2} - \frac{{\sqrt 3 }}{2} = 0\).
Mục 2 của SGK Toán 9 tập 1 - Cánh diều thường xoay quanh các chủ đề về hàm số bậc nhất, hàm số bậc hai và ứng dụng của chúng. Việc nắm vững kiến thức nền tảng về hàm số là vô cùng quan trọng để giải quyết các bài tập trong mục này một cách hiệu quả. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trang 77 và 78, đồng thời phân tích phương pháp giải và những lưu ý quan trọng.
Bài tập này yêu cầu học sinh vận dụng các kiến thức về phương trình bậc nhất một ẩn để tìm ra nghiệm của phương trình. Phương pháp giải thường bao gồm các bước như:
Ví dụ: Giải phương trình 2x + 5 = 0. Ta có x = -5/2.
Để xác định hệ số a của hàm số y = ax + b, học sinh cần sử dụng các thông tin được cung cấp trong đề bài, chẳng hạn như tọa độ của một điểm thuộc đồ thị hàm số. Phương pháp giải:
Ví dụ: Cho hàm số y = ax + 2 và điểm A(1; 5) thuộc đồ thị hàm số. Tìm a. Thay x = 1, y = 5 vào phương trình, ta có 5 = a + 2, suy ra a = 3.
Để vẽ đồ thị hàm số y = ax + b, học sinh cần thực hiện các bước sau:
Ví dụ: Vẽ đồ thị hàm số y = 2x - 1. Ta có hai điểm A(0; -1) và B(1; 1). Vẽ đường thẳng đi qua hai điểm này.
Để tìm giao điểm của hai đường thẳng, học sinh cần giải hệ phương trình bậc nhất hai ẩn tương ứng với hai đường thẳng đó. Phương pháp giải:
Ví dụ: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3. Giải hệ phương trình:
x + 1 = -x + 3
Suy ra 2x = 2, x = 1. Thay x = 1 vào phương trình y = x + 1, ta có y = 2. Vậy giao điểm là (1; 2).
Các bài toán ứng dụng hàm số thường yêu cầu học sinh xây dựng mô hình toán học dựa trên các thông tin được cung cấp trong đề bài, sau đó giải phương trình hoặc hệ phương trình để tìm ra đáp án.
Ví dụ: Một người đi xe máy với vận tốc 40km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km? Ta có hàm số biểu diễn quãng đường đi được là s = 40t, với t là thời gian. Thay t = 2 vào hàm số, ta có s = 80km.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi đối mặt với các bài tập trong mục 2 trang 77, 78 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!