Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 78 sách giáo khoa Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
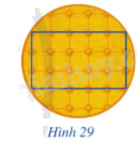
Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.
Đề bài
Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng Định lý Pytago trong tam giác vuông ACB để tính đường kính AC.
Bước 2: Áp dụng công thức \(S = \pi .\frac{{{d^2}}}{4}.\)
Lời giải chi tiết
Mặt trên của tấm nệm được biểu diễn bằng hình học như sau:
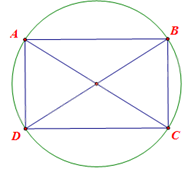
Hình chữ nhật ABCD có chiều dài AB = 5 dm, chiều rộng BC = 3 dm.
Xét tam giác ACB vuông tại B có:
\(\begin{array}{l}A{B^2} + B{C^2} = A{C^2}(Pytago)\\{5^2} + {3^2} = A{C^2}\\AC = \sqrt {34} dm\end{array}\)
Mà hình chữ nhật ABCD nội tiếp đường tròn nên đường kính tấm đệm là \(AC = \sqrt {34} dm.\)
Diện tích hình tròn là: \(S = \pi .\frac{{{d^2}}}{4} = \pi .\frac{{{{\sqrt {34} }^2}}}{4} = \frac{{17\pi }}{2}d{m^2}.\)
Bài tập 4 trang 78 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song.
Bài tập 4 bao gồm các ý nhỏ khác nhau, mỗi ý yêu cầu học sinh thực hiện một thao tác cụ thể liên quan đến hàm số bậc nhất:
Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
a) Cho hàm số y = 2x - 3. Xác định hệ số góc của đường thẳng biểu diễn hàm số.
Giải: Hệ số góc của đường thẳng y = 2x - 3 là a = 2.
b) Cho hai đường thẳng y = -x + 1 và y = -x + 4. Hai đường thẳng này có song song hay không? Vì sao?
Giải: Hai đường thẳng y = -x + 1 và y = -x + 4 có hệ số góc bằng nhau là a = -1, nhưng tung độ gốc khác nhau (1 ≠ 4). Do đó, hai đường thẳng này song song.
c) Tìm giá trị của m để đường thẳng y = (m - 1)x + 2 song song với đường thẳng y = 3x - 5.
Giải: Để hai đường thẳng y = (m - 1)x + 2 và y = 3x - 5 song song, ta cần có hệ số góc bằng nhau, tức là m - 1 = 3. Suy ra m = 4.
Để củng cố kiến thức về hàm số bậc nhất và bài tập 4 trang 78 SGK Toán 9 tập 2 - Cánh diều, bạn có thể tự giải thêm các bài tập sau:
Bài tập 4 trang 78 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các tính chất của nó. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
| Bài tập | Nội dung | Giải pháp |
|---|---|---|
| 4a | Xác định hệ số góc | Tìm hệ số a trong y = ax + b |
| 4b | Kiểm tra tính song song | So sánh hệ số góc và tung độ gốc |
| 4c | Tìm điều kiện song song | Giải phương trình a1 = a2 |