Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 3 trang 34 sách giáo khoa Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Sau khi điều tra về số học sinh trong 100 lớp học (đơn vị: học sinh), người ta có bảng tần số ghép nhóm như ở Bảng 38. a) Tìm tần số tương đối của mỗi nhóm đó. b) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó. c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Đề bài
Sau khi điều tra về số học sinh trong 100 lớp học (đơn vị: học sinh), người ta có bảng tần số ghép nhóm như ở Bảng 38.
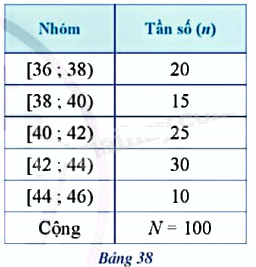
a) Tìm tần số tương đối của mỗi nhóm đó.
b) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.
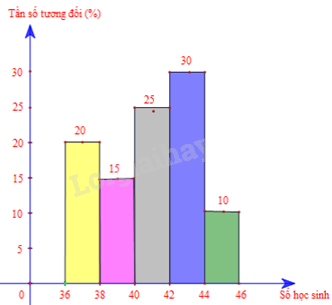
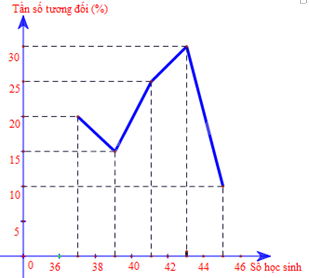
c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Tính tỉ số phần trăm của mỗi tần số.
Lời giải chi tiết
a) Tần số tương đối của các nhóm lần lượt là:
\(\begin{array}{l}{f_1} = \frac{{20}}{{100}}.100\% = 20\% ;{f_2} = \frac{{15}}{{100}}.100\% = 15\% ;{f_3} = \frac{{25}}{{100}}.100\% = 25\% ;\\{f_4} = \frac{{30}}{{100}}.100\% = 30\% ;{f_5} = \frac{{10}}{{100}}.100\% = 10\% \end{array}\)
b) Ta có bảng:

c) Biểu đồ cột:
Biểu đồ đoạn thẳng:
Bài tập 3 trang 34 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song.
Bài tập 3 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để xác định hệ số góc của đường thẳng, ta cần đưa phương trình đường thẳng về dạng y = ax + b, trong đó a là hệ số góc.
Ví dụ: Cho đường thẳng 2x + 3y = 5. Ta có thể viết lại phương trình này như sau:
3y = -2x + 5
y = (-2/3)x + 5/3
Vậy hệ số góc của đường thẳng là -2/3.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song khi và chỉ khi a1 = a2 và b1 ≠ b2.
Ví dụ: Cho hai đường thẳng y = 2x + 1 và y = 2x - 3. Vì hệ số góc của hai đường thẳng bằng nhau (a1 = a2 = 2) và tung độ gốc khác nhau (b1 = 1 ≠ b2 = -3), nên hai đường thẳng này song song.
Để viết phương trình đường thẳng thỏa mãn các điều kiện cho trước, ta cần xác định hệ số góc và tung độ gốc của đường thẳng.
Ví dụ: Viết phương trình đường thẳng đi qua điểm A(1; 2) và song song với đường thẳng y = 3x + 1.
Vì đường thẳng cần viết song song với đường thẳng y = 3x + 1, nên hệ số góc của nó cũng là 3. Vậy phương trình đường thẳng có dạng y = 3x + b.
Thay tọa độ điểm A(1; 2) vào phương trình, ta được:
2 = 3(1) + b
b = -1
Vậy phương trình đường thẳng cần viết là y = 3x - 1.
Kiến thức về hàm số bậc nhất có ứng dụng rộng rãi trong thực tế, chẳng hạn như:
Bài tập 3 trang 34 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng, giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc các em học tốt!
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Hệ số góc | Số a trong phương trình y = ax + b. |
| Đường thẳng song song | Hai đường thẳng không có điểm chung. |