Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài tập 8 trang 87, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Từ vị trí (A) ở phía trên một tòa nhà có chiều cao (AD = 68m), bác Duy nhìn thấy vị trí (C) cao nhất của một tháp truyền hình, góc tạo bởi tia (AC) và tia (AH) theo phương nằm ngang là (widehat {CAH} = 43^circ ). Bác Duy cũng nhìn thấy chân tháp tại vị trí (B) mà góc tạo bởi tia (AB) và tia (AH) là (widehat {BAH} = 28^circ ), điểm (H) thuộc đoạn (BC) (Hình 27). Tính khoảng cách (BD) từ chân tháp đến chân tòa nhà và chiều cao (BC) của tháp truyền hình (làm tròn kết
Đề bài
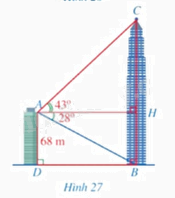
Từ vị trí \(A\) ở phía trên một tòa nhà có chiều cao \(AD = 68m\), bác Duy nhìn thấy vị trí \(C\) cao nhất của một tháp truyền hình, góc tạo bởi tia \(AC\) và tia \(AH\) theo phương nằm ngang là \(\widehat {CAH} = 43^\circ \). Bác Duy cũng nhìn thấy chân tháp tại vị trí \(B\) mà góc tạo bởi tia \(AB\) và tia \(AH\) là \(\widehat {BAH} = 28^\circ \), điểm \(H\) thuộc đoạn \(BC\) (Hình 27). Tính khoảng cách \(BD\) từ chân tháp đến chân tòa nhà và chiều cao \(BC\) của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Lời giải chi tiết
Xét tam giác \(ABD\) vuông tại \(D\) ta có:
\(BD = \frac{{AD}}{{\tan 28^\circ }} = \frac{{68}}{{\tan 28^\circ }} \approx 127,9\left( m \right)\).
Vì AHBD là hình chữ nhật nên \(BH = AD = 68m\), \(AH = BD\).
Xét tam giác \(ACH\) vuông tại \(H\) ta có:
\(CH = AH.\tan 43^\circ \approx 127,9.\tan 43^\circ \approx 119,3\left( m \right)\).
Chiều cao \(BC\) của tháp truyền hình là: \(BC = CH + BH \approx 119,3 + 68 = 187,3\left( m \right)\).
Bài tập 8 trang 87 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài tập 8 bao gồm các ý nhỏ khác nhau, mỗi ý yêu cầu học sinh thực hiện một thao tác cụ thể liên quan đến hàm số bậc nhất. Thông thường, các ý sẽ yêu cầu:
Để giải bài tập 8 trang 87 SGK Toán 9 tập 1 - Cánh diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết cho từng ý của bài tập 8. Ví dụ:)
a) Cho hàm số y = 2x - 3. Tính giá trị của y khi x = 1.
Thay x = 1 vào hàm số, ta được: y = 2 * 1 - 3 = -1.
Vậy, khi x = 1 thì y = -1.
Bài toán: Một cửa hàng bán áo sơ mi với giá 150.000 đồng/chiếc. Gọi x là số áo sơ mi bán được và y là doanh thu của cửa hàng. Hãy viết hàm số biểu thị mối quan hệ giữa x và y.
Giải: Doanh thu của cửa hàng là tích của số áo sơ mi bán được và giá mỗi chiếc áo. Vậy, hàm số biểu thị mối quan hệ giữa x và y là y = 150.000x.
1. Cho hàm số y = -3x + 5. Tính giá trị của y khi x = -2.
2. Viết phương trình hàm số bậc nhất đi qua điểm A(1; 2) và có hệ số a = 3.
3. Giải thích ý nghĩa của hệ số a trong hàm số y = 4x + 1 trong ngữ cảnh bài toán về chi phí vận chuyển.
Bài tập 8 trang 87 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, bạn sẽ có thể giải quyết các bài toán tương tự một cách dễ dàng và hiệu quả.