Bài học này cung cấp kiến thức nền tảng về đường tròn ngoại tiếp và đường tròn nội tiếp tam giác, một chủ đề quan trọng trong chương trình Toán 9 Cánh diều. Chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất, và cách xác định các đường tròn này.
Nội dung bài học được trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể, giúp học sinh nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác đó.
1. Đường tròn ngoại tiếp tam giác
Định nghĩa đường tròn ngoại tiếp tam giác
Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác đó. |
Xác định tâm và bán kính đường tròn ngoại tiếp tam giác
Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường trung trực của tam giác đó. Bán kính đường tròn ngoại tiếp tam giác bằng khoảng cách từ giao điểm ba đường trung trực đến mỗi đỉnh của tam giác đó.
|
Ví dụ:
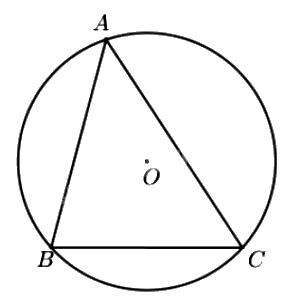
- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O).
- Tâm O là giao điểm của ba đường trung trực của tam giác ABC.
Nhận xét:
- Vì ba đường trung trực của tam giác cùng đi qua một điểm nên tâm đường tròn ngoại tiếp tam giác là giao điểm hai đường trung trực bất kì của tam giác đó.
- Mỗi tam giác có đúng một đường tròn ngoại tiếp.
Đường tròn ngoại tiếp tam giác vuông
Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền.
|
Ví dụ:
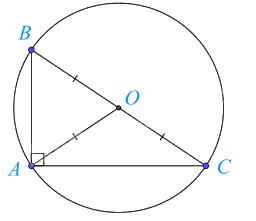
Tam giác ABC nội tiếp đường tròn (O; BO).
Đường tròn ngoại tiếp tam giác đều
- Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn ngoại tiếp của tam giác đó. - Tam giác đều cạnh a có bán kính đường tròn ngoại tiếp là \(R = \frac{{a\sqrt 3 }}{3}\).
|
Ví dụ:
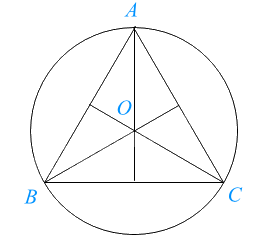
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).
2. Đường tròn nội tiếp một tam giác
Định nghĩa đường tròn nội tiếp tam giác
Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác đó. |
Xác định tâm và bán kính đường tròn ngoại tiếp tam giác
- Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác đó. - Bán kính đường tròn nội tiếp tam giác bằng khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh của tam giác đó. |
Ví dụ:
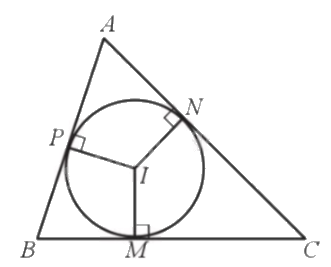
- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).
- Tâm I là giao điểm của ba đường phân giác của tam giác.
Nhận xét:
- Vì ba đường phân giác của một tam giác cùng đi qua một điểm nên tâm đường tròn nội tiếp là giao điểm hai đường phân giác bất kì của tam giác đó.
- Mỗi tam giác có đúng một đường tròn nội tiếp.
Đường tròn nội tiếp tam giác đều
- Trong một tam giác đều, trọng tâm của tam giác đồng thời là tâm đường tròn nội tiếp tam giác đó. - Tam giác đều cạnh a có bán kính đường tròn nội tiếp là \(r = \frac{{a\sqrt 3 }}{6}\).
|
Ví dụ:
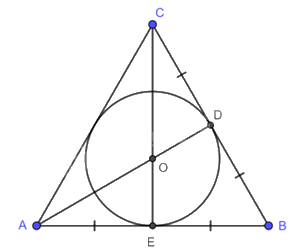
Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).
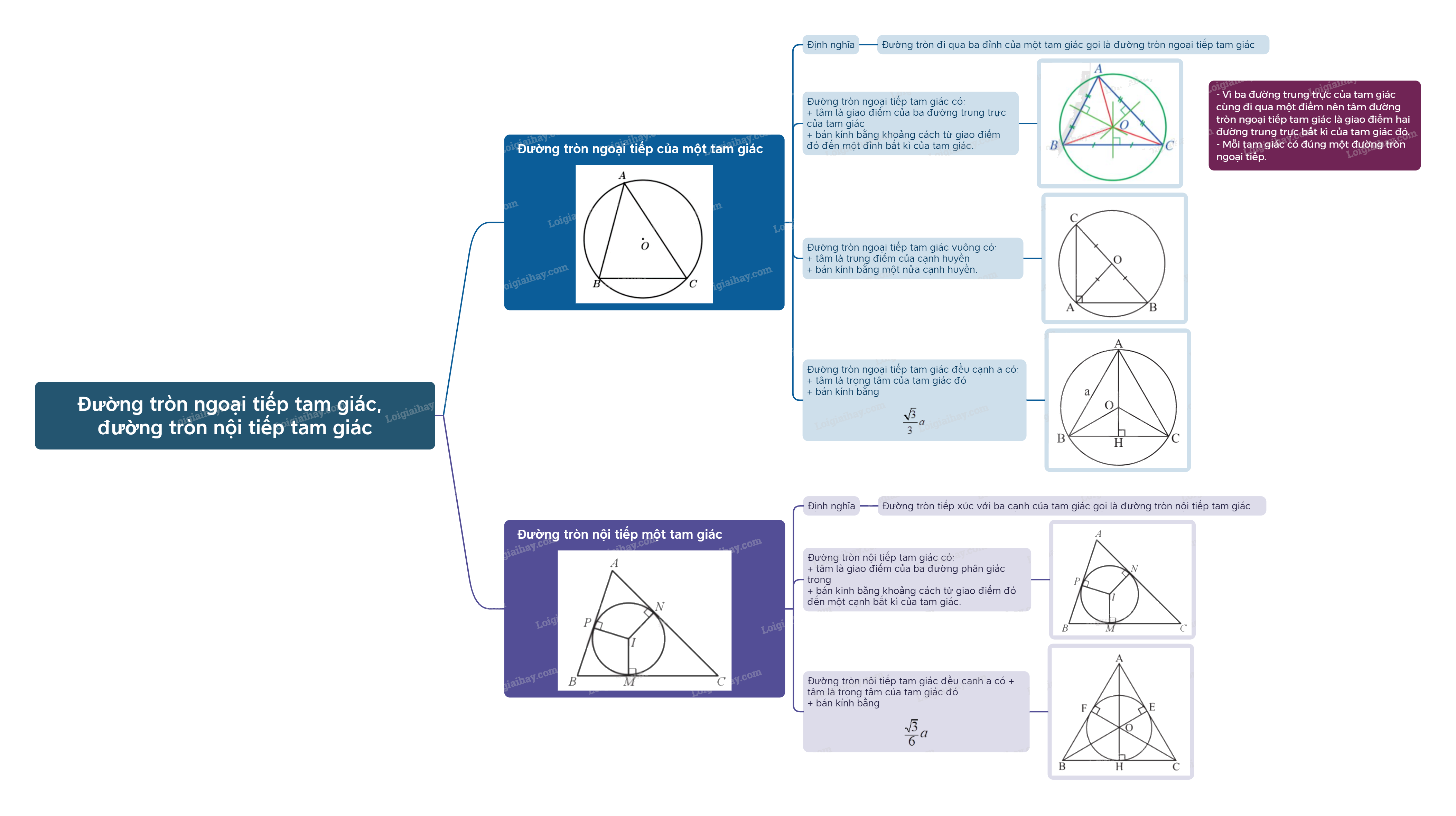
Trong hình học, đường tròn đóng vai trò quan trọng trong việc nghiên cứu các tính chất của tam giác. Hai loại đường tròn đặc biệt liên quan đến tam giác là đường tròn ngoại tiếp và đường tròn nội tiếp. Bài viết này sẽ trình bày chi tiết lý thuyết về hai loại đường tròn này trong chương trình Toán 9 Cánh diều.
Định nghĩa: Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
Tâm đường tròn ngoại tiếp: Giao điểm của các đường trung trực của tam giác là tâm của đường tròn ngoại tiếp tam giác. Tâm này còn được gọi là tâm đường tròn ngoại tiếp.
Bán kính đường tròn ngoại tiếp: Khoảng cách từ tâm đường tròn ngoại tiếp đến mỗi đỉnh của tam giác là bán kính của đường tròn ngoại tiếp, ký hiệu là R.
Công thức tính bán kính đường tròn ngoại tiếp:
Tính chất:
Định nghĩa: Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác đó.
Tâm đường tròn nội tiếp: Giao điểm của các đường phân giác trong của tam giác là tâm của đường tròn nội tiếp tam giác. Tâm này còn được gọi là tâm đường tròn nội tiếp.
Bán kính đường tròn nội tiếp: Khoảng cách từ tâm đường tròn nội tiếp đến mỗi cạnh của tam giác là bán kính của đường tròn nội tiếp, ký hiệu là r.
Công thức tính bán kính đường tròn nội tiếp:
Tính chất:
Đường tròn ngoại tiếp và đường tròn nội tiếp là hai đường tròn quan trọng liên quan đến tam giác. Chúng có mối quan hệ mật thiết với nhau, thể hiện qua các công thức và tính chất đã trình bày ở trên.
Bài 1: Cho tam giác ABC có AB = 3cm, BC = 4cm, CA = 5cm. Tính bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác ABC.
Hướng dẫn:
Bài 2: Chứng minh rằng tâm đường tròn ngoại tiếp của tam giác vuông là trung điểm của cạnh huyền.
Hướng dẫn: Sử dụng tính chất của tam giác vuông và định nghĩa của tâm đường tròn ngoại tiếp.
Việc nắm vững lý thuyết về đường tròn ngoại tiếp và đường tròn nội tiếp tam giác là rất quan trọng để giải quyết các bài toán hình học trong chương trình Toán 9 Cánh diều. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn hiểu rõ hơn về chủ đề này.