Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài tập 7 trang 60 SGK Toán 9 tập 1 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a.
Đề bài
Cho tam giác đều ABC có độ dài cạnh a. Tính độ dài đường cao AH của tam giác ABC theo a.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Kết hợp với các kiến thức hình học cùng phép tính của căn thức để giải bài toán
Lời giải chi tiết
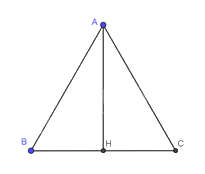
Do AH là đường cao của tam giác đều ABC.
Suy ra AH đồng thời là đường trung tuyến của tam giác ABC.
Suy ra H là trung điểm của BC.
Suy ra \(HB = HC = \frac{1}{2}BC = \frac{1}{2}a\).
Xét tam giác AHB vuông tại H có:
\(A{H^2} + H{B^2} = A{B^2}\) (Định lý Py – ta – go)
\(\begin{array}{l}A{H^2} + {\left( {\frac{a}{2}} \right)^2} = {a^2}\\A{H^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = {a^2} - \frac{{{a^2}}}{4} = \frac{{4{a^2}}}{4} - \frac{{{a^2}}}{4} = \frac{{3{a^2}}}{4}\\AH = \frac{{a\sqrt 3 }}{2}.\end{array}\)
Vậy \(AH = \frac{{a\sqrt 3 }}{2}\).
Bài tập 7 trang 60 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và ứng dụng của chúng trong giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài tập 7 yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Để vẽ đồ thị của hàm số bậc nhất y = ax + b, ta cần xác định hai điểm thuộc đồ thị. Thông thường, ta chọn hai điểm có hoành độ bằng 0 và 1. Sau đó, nối hai điểm này lại với nhau, ta được đồ thị của hàm số.
Để xác định một điểm thuộc đồ thị của hàm số y = ax + b, ta thay hoành độ của điểm đó vào phương trình hàm số để tìm tung độ. Ví dụ, nếu ta muốn xác định điểm có hoành độ bằng 2, ta thay x = 2 vào phương trình hàm số để tìm y.
Để tìm tọa độ giao điểm của đồ thị hàm số với trục Ox, ta cho y = 0 và giải phương trình ax + b = 0 để tìm x. Tọa độ giao điểm là (x, 0).
Để tìm tọa độ giao điểm của đồ thị hàm số với trục Oy, ta cho x = 0 và tìm y. Tọa độ giao điểm là (0, y).
Trong các bài toán thực tế, hàm số bậc nhất thường được sử dụng để mô tả mối quan hệ giữa hai đại lượng. Để giải quyết các bài toán này, ta cần xác định hàm số phù hợp và sử dụng các kiến thức về hàm số bậc nhất để tìm ra đáp án.
Giả sử ta có hàm số y = 2x + 1. Hãy vẽ đồ thị của hàm số này và tìm tọa độ giao điểm của đồ thị với các trục tọa độ.
Lời giải:
Khi giải bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Bài tập 7 trang 60 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải quyết bài tập và đạt kết quả tốt trong môn Toán.