Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Bài tập 2 thuộc chương trình học Toán 9 tập 1, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi hy vọng với sự hỗ trợ này, các em sẽ có những giờ học Toán 9 hiệu quả và thú vị.

Cho đường tròn (left( {O;R} right)) và dây (AB) sao cho (widehat {AOB} = 90^circ ). Giả sử (M,N) lần lượt là các điểm thuộc cung lớn (AB) và cung nhỏ (AB) ((M,N) khác (A) và (B)). a) Tính độ dài đoạn thẳng (AB) theo (R). b) Tính số đo các góc (ANB) và (AMB).

Đề bài

Cho đường tròn $\left( {O;R} \right)$ và dây $AB$ sao cho $\widehat {AOB} = 90^\circ $. Giả sử $M,N$ lần lượt là các điểm thuộc cung lớn $AB$ và cung nhỏ $AB$ ($M,N$ khác $A$ và $B$).

a) Tính độ dài đoạn thẳng $AB$ theo $R$.

b) Tính số đo các góc $ANB$ và $AMB$.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều 1

Dựa vào tính chất góc ở tâm và góc nội tiếp để tính.

Lời giải chi tiết

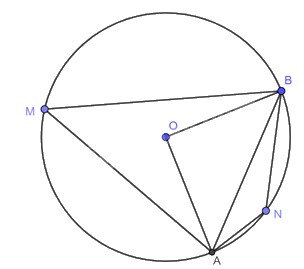Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều 2 a) Áp dụng định lí Pythagore vào tam giác $AOB$ vuông tại $O$, ta có:

$O{A^2} + O{B^2} = A{B^2} \Rightarrow A{B^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AB = R \sqrt 2$

b) Xét đường tròn $\left( O \right)$:

+) Vì M thuộc cung lớn AB nên $\widehat {AMB}$ là góc nội tiếp và $\widehat {AOB}$ là góc ở tâm cùng chắn cung nhỏ $AB$ nên:

$\widehat {AMB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.90^\circ = 45^\circ $.

+) Số đo cung lớn AB là:

$sđ\overset\frown{AB}\; lớn=360{}^\circ - sđ\overset\frown{AB }\; nhỏ=360{}^\circ -90{}^\circ =270{}^\circ $

+) Vì N thuộc cung nhỏ AB nên $\widehat {ANB}$ là góc nội tiếp chắn cung lớn $AB$ nên:

$\widehat{ANB}=\frac{1}{2}sđ\overset\frown{AB }\; lớn=\frac{1}{2}.270{}^\circ =135{}^\circ $.

Vậy $\widehat {AMB} = 45^\circ ,\widehat {ANB} = 135^\circ $.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều đặc sắc thuộc chuyên mục toán 9 sgk trên nền tảng môn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều: Hướng dẫn chi tiết và phương pháp giải

Bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các vấn đề thực tế. Dưới đây là hướng dẫn chi tiết và phương pháp giải bài tập này:

Phần 1: Đề bài và phân tích

Trước khi đi vào giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài tập 2 thường yêu cầu học sinh:

Xác định hàm số bậc nhất hoặc hàm số bậc hai.
Tìm các hệ số của hàm số.
Vẽ đồ thị của hàm số.
Giải các bài toán liên quan đến đồ thị hàm số (ví dụ: tìm giao điểm, tìm giá trị của hàm số tại một điểm).

Phần 2: Phương pháp giải

Để giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều, chúng ta có thể áp dụng các phương pháp sau:

Phương pháp xác định hàm số: Sử dụng các công thức và định nghĩa về hàm số bậc nhất và hàm số bậc hai để xác định hàm số.
Phương pháp tìm hệ số: Thay các điểm thuộc đồ thị hàm số vào phương trình hàm số để tìm các hệ số.
Phương pháp vẽ đồ thị: Xác định các điểm đặc biệt trên đồ thị (ví dụ: giao điểm với trục hoành, trục tung, đỉnh của parabol) và vẽ đồ thị.
Phương pháp giải bài toán liên quan đến đồ thị: Sử dụng các kiến thức về đồ thị hàm số để giải quyết các bài toán.

Phần 3: Lời giải chi tiết

Bài tập 2a: (Ví dụ về một bài tập cụ thể, giả sử là tìm hệ số của hàm số y = ax + b đi qua hai điểm A(1; 2) và B(-1; 0))

Để tìm hệ số a và b, ta thay tọa độ của hai điểm A và B vào phương trình hàm số:

Thay A(1; 2): 2 = a * 1 + b
Thay B(-1; 0): 0 = a * (-1) + b

Giải hệ phương trình này, ta được a = 1 và b = 1. Vậy hàm số cần tìm là y = x + 1.

Bài tập 2b: (Ví dụ về một bài tập cụ thể, giả sử là vẽ đồ thị hàm số y = x² - 4x + 3)

Để vẽ đồ thị hàm số y = x² - 4x + 3, ta thực hiện các bước sau:

Tìm tọa độ đỉnh của parabol: x_đỉnh = -b / 2a = 2; y_đỉnh = (2)² - 4 * 2 + 3 = -1. Vậy đỉnh của parabol là (2; -1).
Tìm giao điểm với trục hoành: Giải phương trình x² - 4x + 3 = 0, ta được x₁ = 1 và x₂ = 3. Vậy giao điểm với trục hoành là (1; 0) và (3; 0).
Tìm giao điểm với trục tung: Thay x = 0 vào phương trình hàm số, ta được y = 3. Vậy giao điểm với trục tung là (0; 3).
Vẽ đồ thị parabol đi qua các điểm đã tìm được.

Phần 4: Lưu ý khi giải bài tập

Khi giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều, các em cần lưu ý:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Sử dụng đúng các công thức và định nghĩa.
Kiểm tra lại kết quả sau khi giải xong.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.

Phần 5: Bài tập tương tự

Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Toán 9 tập 1 - Cánh diều. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.

Hy vọng với hướng dẫn chi tiết này, các em sẽ giải quyết thành công bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều và đạt kết quả tốt trong môn Toán.